WAGNER RODRIGUES POETA E CRONISTA

APÊNDICE

A função exponencial y = e^x tem a intrigante e única propriedade de ser sua própria derivada, i.e.:

d e^x /dx = e^x. Isso é mais uma definição que uma propriedade única. Dessa forma, pode-se definir que que só existe um único número maior que zero que satisfaça a equação ln(x)   , sendo esse x igual a “e”. Portanto  também define o número neperiano e.

 Prova de que: e^x = lim _n->∞[(1 + x / n) ⁿ]^x

Primeiramente vamos provar que: e= lim _n->∞[(1 + 1 / n) ⁿ]

Para isto vamos chamar h=1/n para transformar a equação acima em:

e= lim _h->0 [(1 + h) ^1/h]

Para fazer esta demonstração vamos utilizar a definição de derivada da função f(x)=ln.

Pela definição de logaritmo, d.ln(x)/dx=1/x e para x=1 temos que:

f’(x)=1/1=1

Assim lim _h->0 {[ln(1 + h)– ln(1)]/h} e como ln(1) = 0 (pois e⁰=1) simplificamos:

1 = lim _h->0 [(1/h).ln(1 + h)] e usando a propriedade dos logaritmos de que ln x^r=r.ln x , pois se ln x^r=B => (e^B = x^r ) ou que (e^B/r = x) assim ln(x)=B/r ou que r.ln(x)=B= ln x^r

temos: 1 = lim _h->0 [ln(1 + h)]^1/h e considerando a continuidade da função logarítmica que define que se lim ln f(x) = ln lim f(x)

temos: 1 = ln { lim _h->0  [(1 + h)^1/h ] }

e como por definição ln e = 1 temos que:  ln e = ln{ lim _h->0  [(1 + h)^1/h ]}

portanto:  e = lim _h->0  [(1 + h)^1/h ] ou ainda: e = lim _n->∞[(1 + 1 / n) ⁿ]”

 lim _n->∞[(1 + x / n) ⁿ]^x  = lim _n->∞{[1 + 1/(n/x)] ^n/x}^x  e chamando n/x de n’:

lim _n->∞{[1 + 1/n’)^n’}^x  = { lim _n->∞ [1 + 1/n’)^n’}^x  = e^x portanto:

e^x = lim _n->∞[(1 + x / n) ⁿ]^x 

Que também pode ser escrito como:

e^x = lim _h->0[(1 + x / n)^1/h]^x 

Outra demonstração da Derivada da Função Exponencial (d/dx e^x= e^x)

Esta demonstração foi extraída do site:

http://obaricentrodamente.blogspot.com.br/2009/07/demonstracao-derivada-da-funcao.html)

Está dividida em duas partes, para melhor esclarecimento:

a) Para iniciar esta demonstração, vamos primeiramente provar, de uma outra forma, o limite abaixo:

Por Hipótese:

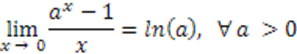
Para a ≠ 1, fazemos uma mudança de variável:

a^x – 1 = t  

Se x tende a zero, então t tende a zero também, pois:

a⁰ – 1 = t

1 – 1 = t

t = 0

Fazemos então:

a^x = 1 + t  

Assim podemos escrever:

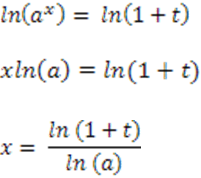
Então, tomando o limite inicial:

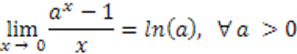
Aplicamos a mudança da variável x para t: Pela demonstração do limite fundamental exponencial, o limite abaixo tende a e:

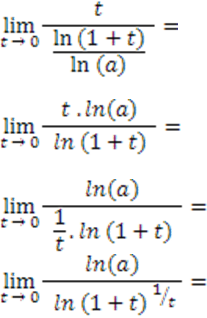
Então, aplicando o limite, obtemos:

ln(a) / ln(e) = ln(a) /1 = ln (a)

Como queríamos demonstrar, comprovando a afirmação inicial.

b) Utilizando o conceito de derivada , temos:

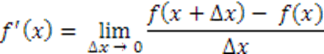
Para uma função exponencial do tipo:

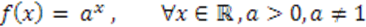
Fazemos as devidas substituições:

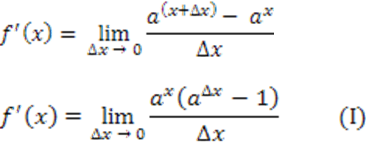
Provamos em a) que o limite:

Aplicando o limite acima, podemos reescrever ( I ) como:

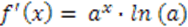
Portanto, podemos dizer que, se:

Mas, se a = e, temos:

Outra demonstração do Limite Fundamental Exponencial

Esta demonstração também  foi extraída do site:

http://obaricentrodamente.blogspot.com.br/2009/07/demonstracao-derivada-da-funcao.html)

O número e tem grande importância em diversos ramos das ciências, pois está presente em vários fenômenos naturais como por exemplo: crescimento populacional, crescimento de população de bactérias, datação do carbono, circuitos elétricos, entre outros.

Foi John Napier (1550-1617), matemático escocês, o responsável pelo desenvolvimento da teoria logarítmica utilizando o número e como base. O número e é irracional e vale aproximadamente:

e = 2,7182818…

Devido à sua vasta aplicação, a função exponencial f (x) = e^x é considerada uma das funções mais importantes da matemática.

Seja o limite exponencial:

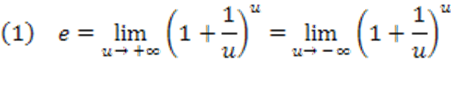
Vamos fazer uma mudança de variável, onde:

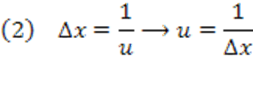
Logo, substituindo (2) em (1), obtemos:

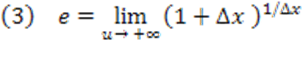
Vejam que u→+∞ quando Δx→0+ e que u→−∞ quando Δx→0−. Assim, as equações podem ser escritas como:

Ou simplesmente:

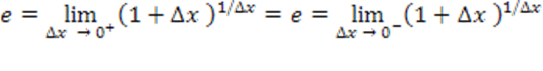
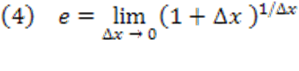
Consideremos o fato que um número:

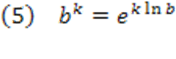
Sendo válido para todos os valores reais de k e sendo b > 0. (Veja seção de Funções Exponenciais e Logarítmicas com Bases Diferentes de e, Munem – Foulis, pág 445).

Assim:

A prova se dará quando:

Pois, então:

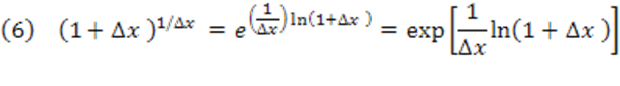
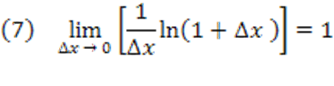
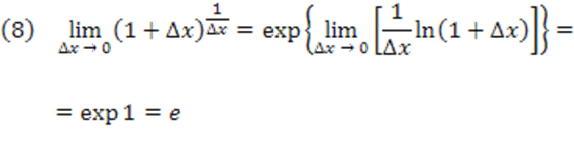
virá como continuidade da função exponencial.

Podemos provar o limite dado em (7). Para isso, façamos:

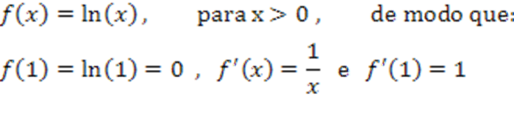
Assim:

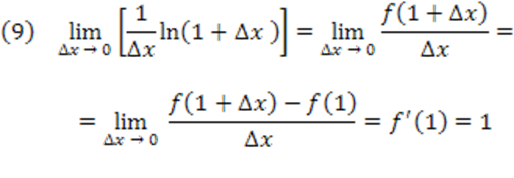
Utilizando-se do teorema dado em (1), podemos estabelecer:

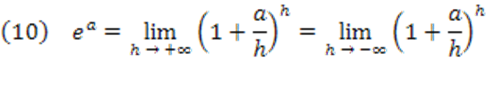
Quando a>0, façamos u=h/a, observando que u→+∞ quando h→+∞. Portanto:

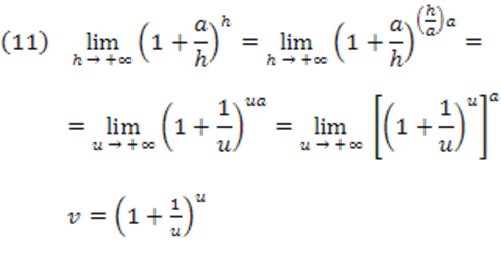
Façamos, então:

Para a verificação, podemos usar noções de série e utilizaremos uma tabela de aproximações:

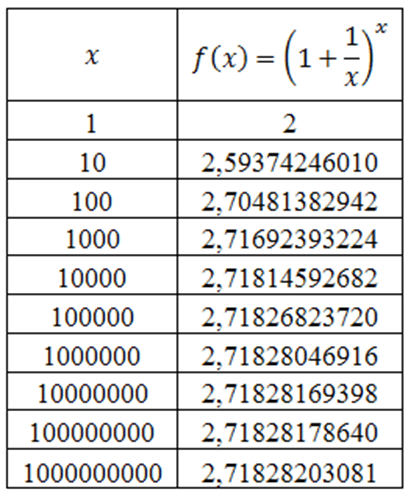
Então, se:

1/x = u => x = 1/u

Se x→∞, então t→0, logo:

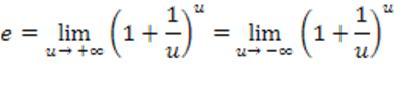
Referências:

[1] Cálculo com Geometria Analítica – Munem – Foulis

BIBLIOGRAFIA

Principles of Corporate Finance Richard A. Breadey and Steward C. Myers
Financial Market and Corporate Finance Mark Griblatt and Sheridan Titman
Fundamentals of Financial Management Eugene F. Brigham
Economics Paul A. Samuelson
Managerial Finance J. Fred Weston and Eugene F. Brigham
The Capital Budgeting Decision – Economic Analysis of Investment Projects Harold Biermam Jr and Seymor Smidt
Valuation – Measuring Manging the Value of Companies Tom Coperland, Tim Koller and Jack Murrin
Analysis for Financial Management Robert C. Higgins
Macroeconomics N. Gregory Mankiw
Calculus and Analytic Geometry Abe Mizrahi and Michael Sullivan
Cálculo com Geometria Analítica Munem – Foulis
Business Analysis and Valuation – Using Financial Statements Krisna G. Papelu, Paul M. Healy and Victor L. Bernard