PARTE IV – CONCEITOS DE TAXAS DE ATRATIVIDADE E PRINCÍPIOS DA VALORIZAÇÃO BASEADOS EM RISCO

Objetivo do Capítulo sobre Taxas de Descontos e Risco

Numa empresa, o que define a taxa de oportunidade (ou de desconto) com a qual uma empresa deve avaliar o valor do dinheiro ao longo do tempo (fluxo de caixa), por exemplo, de um projeto, é o custo dessa empresa se financiar. Uma empresa saudável necessita considerar remunerar o investimento feito de forma a superar esse custo. Para uma empresa criar valor é necessário que os investimentos propiciem uma TIR (taxa interna de retorno) que supere esse custo do financiamento em seus projetos e no seu todo.

Existem muitas e variadas formas de financiar uma empresa. Algumas dessas formas podem estar no próprio lado operacional da empresa, quando esta recorre a seus fornecedores e até a seus funcionários alongando os prazos de pagamento. Como o custo desse tipo de financiamento não existe, ou está embutido em outras variáveis como no preço mais alto de um insumo comprado, a forma como a avaliação econômica trata do assunto é definir que houve uma diminuição na necessidade de investir. Esse tipo de financiamento não precisa ser remunerado e não compõe a taxa de desconto da empresa, já que o custo deste financiamento está embutido nos custos (desembolsos de caixa), como no preço dos insumos comprados.

Quando nos referimos à taxa de desconto ou custo do financiamento de uma empresa, estamos nos referindo aos investimentos através de acionistas e outros financiadores de mais longo prazo (bancos ou similares) que, respectivamente, esperam ou cobram um retorno.

Quando o financiamento é feito mediante uma remuneração pré-estabelecida, mediante o retorno do principal e uma taxa de juros cobrada de forma independente da lucratividade e, com efeito fiscal positivo sobre este custo, dizemos que o financiamento foi feito através de uma dívida. Exemplos são os empréstimos bancários de curto e longo prazo, empréstimos feitos por acionistas ou empresas coligadas, mediante uma taxa de juros definida a ser paga periodicamente, debentures lançadas no mercado pelas empresas, e outras.

Quando o financiamento é feito pelo dono, ou acionistas da empresa, cujo retorno é condicional à existência de lucro e decisão da empresa distribuir dividendos, dizemos que o financiamento é através de capital próprio.

Uma forma intermediária de financiamento é feito através de emissão de ações preferenciais. Ações preferenciais podem ter menor risco, estabelecido por contrato, que as ações ordinárias. Entretanto não têm efeito fiscal positivo (ou seja, seu custo não tem fator redutor do imposto de renda a ser pago), são condicionais à existência de lucro acumulado e podem ser limitados a uma determinada taxa de remuneração, como são os juros (de novo, exceto pelo fator fiscal).

Enquanto o custo da dívida é pré-definido e relativamente fácil de ser apurado, entender o custo do capital próprio (ou custo do equity) é bem mais complicado e bem menos objetivo.

Custo do Capital Próprio (Custo do Equity)

O investidor em equity (seja o dono, seja o acionista direto ou o acionista que negocia ações de empresa no mercado secundário) busca um retorno o maior possível. Como esse investidor dependerá da lucratividade da empresa para ter esse retorno (através de dividendos), ele acaba tendo um risco maior que o risco que tem os financiadores da dívida.

Não existe um custo negociado para o financiador do capital próprio. São as alternativas de investimento do investidor em outras ações que formam a base da definição do custo do equity da empresa. Em outras palavras, a empresa necessita estar competitiva do ponto de vista de retorno e risco para atrair investidores quando buscam um aumento de capital através de venda de ações ordinárias da empresa.

O custo do capital próprio é, portanto, função das alternativas que tem os donos da empresa de investir em outras ações disponíveis no mercado, cada qual com seu risco próprio. Essa opção é o que vai definir o custo ou a ganho alternativo de se investir na própria empresa.

Numa empresa existente, esta é uma forma marginal de se aumentar o patrimônio da empresa, pois, a primeira opção seria reter lucros gerados ao invés de distribuí-los como dividendos. Para o investidor no capital próprio da empresa existe a possibilidade de vender as ações da empresa e investir em qualquer outra do mercado, através da compra de ações.

Entender o valor dessas alternativas e o risco dessas alternativas é o que irá definir o custo do patrimônio líquido ou equity.

Para iniciar esta análise vamos entender um pouco dos princípios do investimento em ações.

Investimento em Ações

Investir em ações implica em provavelmente ganhar mais dinheiro no longo prazo sem nunca saber quando ou se de fato este ganho irá ocorrer. É um jogo de risco e retorno e de eventuais perdas.

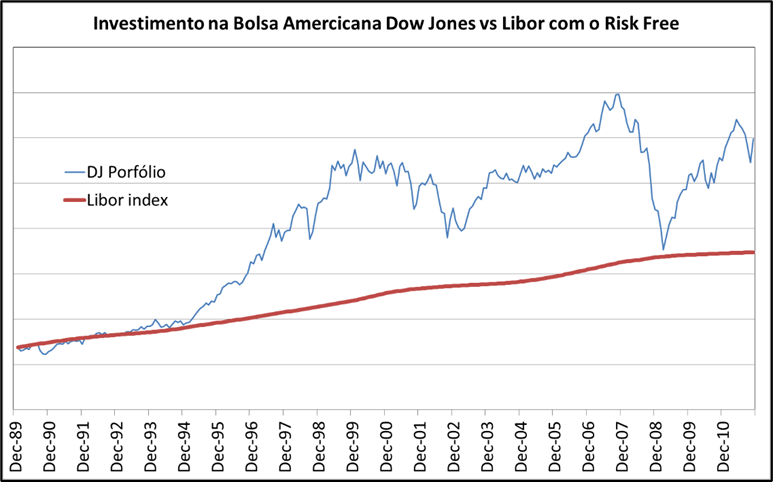
O estudo dessa variável é mais complexo do que é necessário aos executivos que tomam decisão na empresa e mesmo à maioria dos bons avaliadores econômicos. Entretanto penso que seja útil, ao menos, que entendam os princípios em que esse estudo se baseia.

Mesmo sem pretender rigor acadêmico, vamos nos arriscar nesta empreitada.

As ideias apresentadas por Harry Markovisky no início dos anos 50 formam a base da discussão da formação de portfólios.

Esses estudos mostraram que os investidores poderiam reduzir a volatilidade de seus investimentos escolhendo ações que se movem de forma desalinhada. Por exemplo, existem ações que tem por base o comportamento da economia, como a indústria de distribuição de energia. Outras ações voltadas a novas tecnologias e novos mercados podem ter comportamentos diferentes, como tiveram a então emergente indústria da computação e mais tarde a de softwares, depois a Google e os vários sites de relacionamento, os sites de compras na internet, entre outros.

Segundo essas ideias, a distribuição dos rendimentos das ações apresenta um comportamento semelhante ao de uma curva normal. Assim, por ser uma curva normal, o comportamento do rendimento das ações pode ser completamente definido por apenas duas variáveis estatísticas: O “Retorno Médio Esperado” e o seu “Desvio Padrão”.

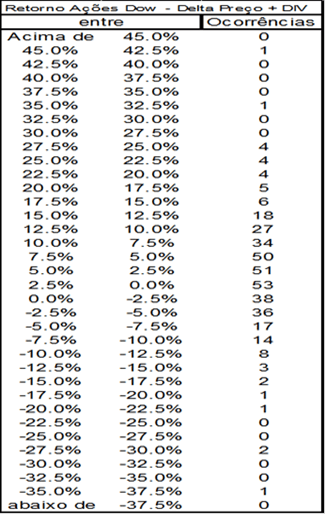
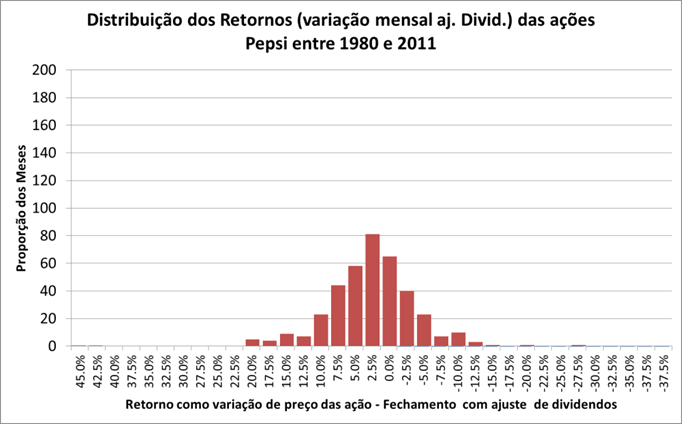
Na (Figura 16) temos os resultados históricos da variação dos fechamentos das ações da The Dow Chemical Co, ajustados com as distribuições de dividendos, baixadas do site Yahoo Finance entre Janeiro de 1980 e Novembro de 2011.

De fato essa distribuição é próxima de uma normal:

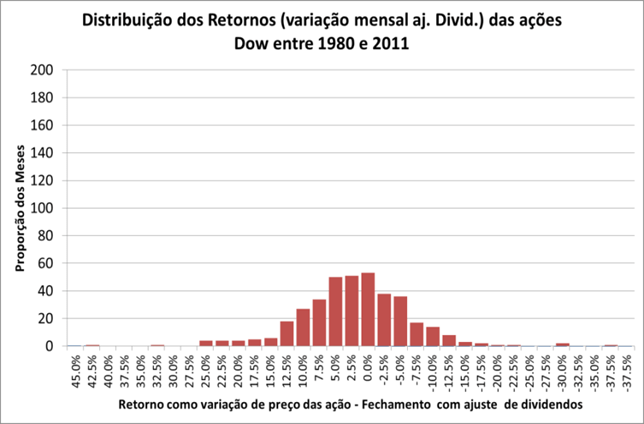
Assim, tomando-se como base o período, Jan de 1980 e Novembro de 2011, as ações da Dow podem ser razoavelmente representadas por: (a) Um Retorno Médio Esperado de 1.14% ao mês; e (b) Seu desvio padrão de 9,8% ao mês. Da estatística, devemos nos lembrar de que na distribuição normal, Variância e Desvio Padrão são calculados pelas fórmulas:

Variância =∑ (retornos mensal – média dos retornos mensais)² / (n^o de meses -1)

Desvio Padrão = Variância^1/2

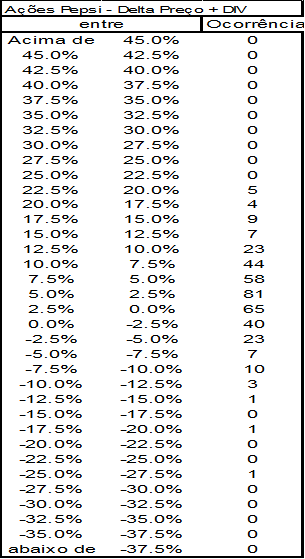
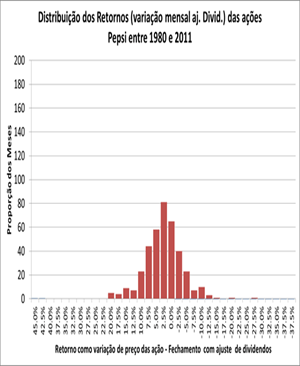
Façamos o mesmo com ações da Pepsi Co, conforme tabela da (Figura 18).

Notamos uma maior concentração dos valores que significa uma menor volatilidade, menor risco, com relação aos retornos da Dow.

Se o retorno médio for igual ao retorno médio da Dow, significa que o investidor irá preferir ações da Pepsi às Ações da Dow.

Assim como com as ações da Dow, os retornos das ações da Pepsi apresentam uma distribuição normal, e, portanto, também podem ser totalmente definidas pelo seu Retorno Esperado e o Desvio Padrão desse retorno.

Dessa forma, tomando-se como base o período, Jan de 1980 e Novembro de 2011, as ações da Pepsi podem ser representadas por: (a) um Retorno Médio Esperado de 1.41% ao mês, e (b) Seu desvio padrão de 6,2% ao mês.

Se aceitarmos essa longa experiência histórica como um bom proxy das expectativas futuras, temos que individualmente os retornos das ações da Dow e da Pepsi podem ser definidos por seus parâmetros estatísticos:

Ação Dow (Retorno Esperado de 1,14% ao mês e Desvio Padrão de 9,8% ao mês)

Ação Pepsi (Retorno Esperado de 1,41% ao mês e Desvio Padrão de 6,2% ao mês)

Se tomarmos um período 10 anos mais recente, por exemplo, entre Janeiro de 1990 e Novembro 2011, esses mesmos parâmetros mudam um pouco, mas mantém sua relatividade. Ainda poderíamos mudar a periodicidade (semestral, anual, diária) e teríamos dados relativamente semelhantes:

Ação Dow (Retorno Esperado de 0,89% ao mês e Desvio Padrão de 10,56% ao mês)

Ação Pepsi (Retorno Esperado de 1,05% ao mês e Desvio Padrão de 6,1% ao mês)

Assim percebemos diferentes períodos da história indicam que a ação da Pepsi apresenta um retorno maior e com menor volatilidade (desvio padrão) que a ação da Dow.

Já podemos perceber que estamos na área das probabilidades ao definir custo do capital próprio, e não no campo das certezas.

Formação de Portfólios – Introdução das Variáveis Estatísticas

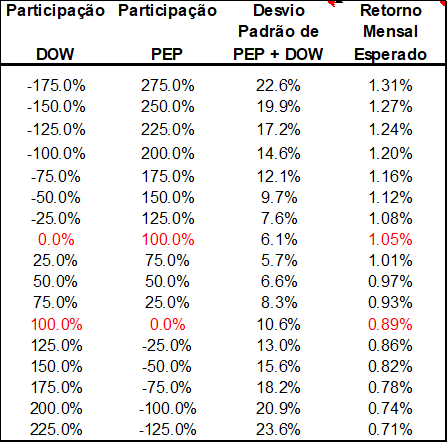
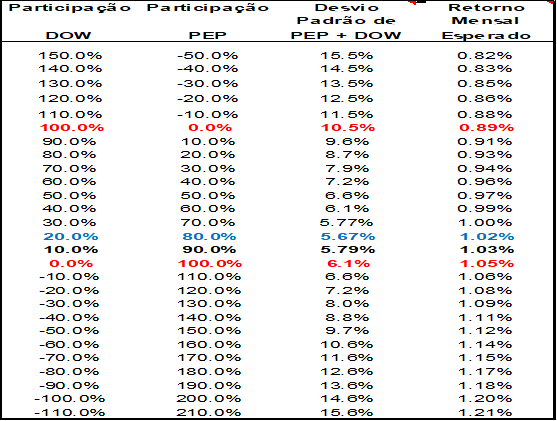
Tomemos o período Janeiro de 1990 e Novembro de 2011 e vamos combinar ações da Dow e da Pepsi em diversas porcentagens e criar uma série de portfólios que gerariam diferentes parâmetros de Retorno Médio e Desvio Padrão.

Na (Figura 20) vemos que é possível ficar “vendido” em ações Dow (participação negativa) compensada com “comprado” em ações Pepsi, e vice-versa, de tal forma a formar todos os portfólios do quadro. Obviamente a soma do portfólio é sempre 100% do investimento, ou seja, do valor que está disponível para se investir.

A Média do Retorno dos portfólios tem um resultado relativamente intuitivo, pois é a média ponderada das médias de retornos mensais dos dois papéis. É intuitivo, mas sua demonstração não é imediata. Faremos esta demonstração na sequência.

Importante! Formar o Portfólio Dow e Pepsi não se trata de manter no portfólio um número fixo de ações da Dow e Pepsi a partir de uma aplicação inicial. É necessário ajustar mensalmente o portfólio, vendendo ações que subiram mais que a outra e comprando ações que subiram menos, de tal forma a sempre manter os montantes monetários na proporção desejada.

O outro parâmetro que irá definir completamente o Portfólio, o desvio padrão (DP), tem um cálculo menos intuitivo, conforme veremos.

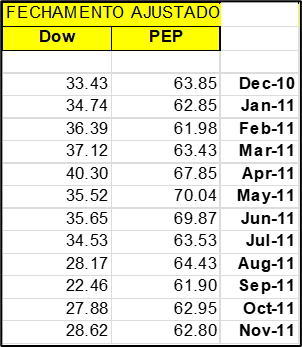
Vamos seguir um exemplo prático, tomando somente os resultados mensais do ano de 2011 (janeiro a novembro de 2011) para deixar mais claro como tratar as variáveis estatísticas.

Na ( Figura 21) vemos os resultados publicados por “Yahoo Finance” dos fechamentos mensais ajustados com distribuição de dividendos das ações da Pepsi e da Dow na bolsa de NY.

Agora vamos montar um portfólio com X de montante monetário e investi-lo em ações Dow e o restante (1-X) em ações Pepsi.

Vamos chamar de x’ o quociente das de ações Dow sobre o total de ações. Assim, como o preço das ações Dow e Pepsi tem valores diferentes podemos calculá-lo a partir de X, e vice-versa.

Usaremos P = preço da Pepsi em cada mês e D = preço da ação da Dow em cada mês.

Em todo momento teremos que

X = D × x’ / ( P × (1 – x’) + D × x’)

Agora vamos promover algumas operações algébricas com esta equação:

X = D × x’ / (P – P × x’ + D × x’)

1 / X = (P – P × x’ + D × x’) / D × x’

1 / X = P/ D × x’ – P × x’ / D × x’ + D × x’ / D × x’

1 / X = P/ D×x’ – P × x’ / D × x’ + 1

1 / X – 1 = P / D × x’ – P × x’ / D × x’

1 / X – 1 = P/ D × x’ – P / D

1 / X – 1 + P / D = P / D × x’

(D / X – D + P) / D = P / D × x’

D × x’ = P × D / (D/X – D + P)

x’ = P / (D/X – D + P), lembrando x’ o quociente do n^o de ações Dow sobre o total de ações.

Assim, em dezembro de 2010 (veja os preços no quadro anterior), se escolhermos que X=40%, ou seja, que vamos investir 40% do montante monetário em ações Dow, teremos que comprar x’ ações Dow e (1-x’) ações Pepsi. Portanto compraríamos:

x’ = P / (D/X – D + P)

x’ = 63,85 / (33,43/40% – 33,43 + 63,85) = 56,0%

Ou seja, 56% do número total de ações seriam compradas em ações Dow e o restante em ações Pepsi. Assim, se tivéssemos US$100M investiríamos US$100M × X = US$40M em ações da Dow (compraríamos US$40M/US$33,43 = 1196,5 ações Dow).

Consequentemente o restante US$60M em ações Pepsi (compraríamos US$60M/US$63,85 = 939,7 ações Pepsi). O total de ações seria 1196,5 + 939,7 = 2136,2 ações. De fato, o percentual de ações Dow seria de 1196,5/2136,2 = 56%.

Com a variação de preço das ações, no final de janeiro de 2011, para mantermos 40% do montante investidos em ações Dow, será necessário vender algumas ações da Dow e comprar da Pepsi uma vez que em janeiro o preço da ação da Dow teve um aumento e a Pepsi uma redução. Esse ajuste deve ser feito para que a equação x’ = P / (D/X – D + P) seja observada a partir do início de fevereiro de 2011.

x’ = P / (D/X – D + P)

x’ = 62,85 / (34,74/40% – 34,74 + 62,85) = 54,7% do total de ações em ações Dow.

Investimos inicialmente US$100.000,00 comprando 1196,5 ações Dow e 939,7 ações Pepsi. Aos preços de final de janeiro de 2011 teríamos US$100.627,75 e teríamos que ter 40% ou US$40251,10 em ações Dow que então valem US$34,74. Assim teríamos que ter 1158,64 ações Dow. Como tínhamos 1196,5 devemos vender 37,89 ações da Dow a US$34,74 cada e apuraríamos US$1316,35 que compraríamos em ações da Pepsi a US$62,85 cada ou 1136,35/62,85 = 20,94 ações Pepsi. Assim ficaríamos com 939,7 + 20,94 = 960,65 ações Pepsi. Dessa forma o total de ações seria 1158,64 + 960,65 = 2119,29 ações. De fato, o percentual de ações Dow seria de 1158,64/2119,29= 54,7%.

Na (Figura 22) vemos o resumo desses cálculos feitos para o período que estamos usando como exemplo com 40% do montante monetário aplicado cada e todo mês em ações Dow e o restante em ações Pepsi:

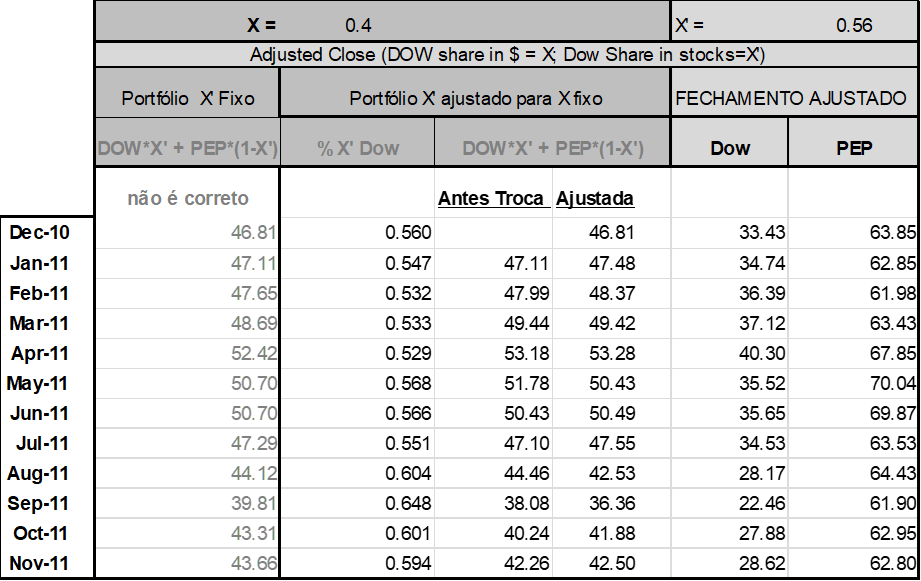
No quadro seguinte (Figura 22) apresentamos dois métodos de cálculo do retorno mensal médio do Portfólio com 40% do montante monetário aplicado cada e todo mês em ações Dow e o restante em ações Pepsi. A primeira coluna da (Figura 22) apenas mostra aquilo que estatisticamente não deve ser feito, ou seja, imaginar que os percentuais das ações é o que se mantem ao longo do tempo. Estatisticamente temos que usar as opções na periodicidade escolhida, como a partir da segunda coluna.

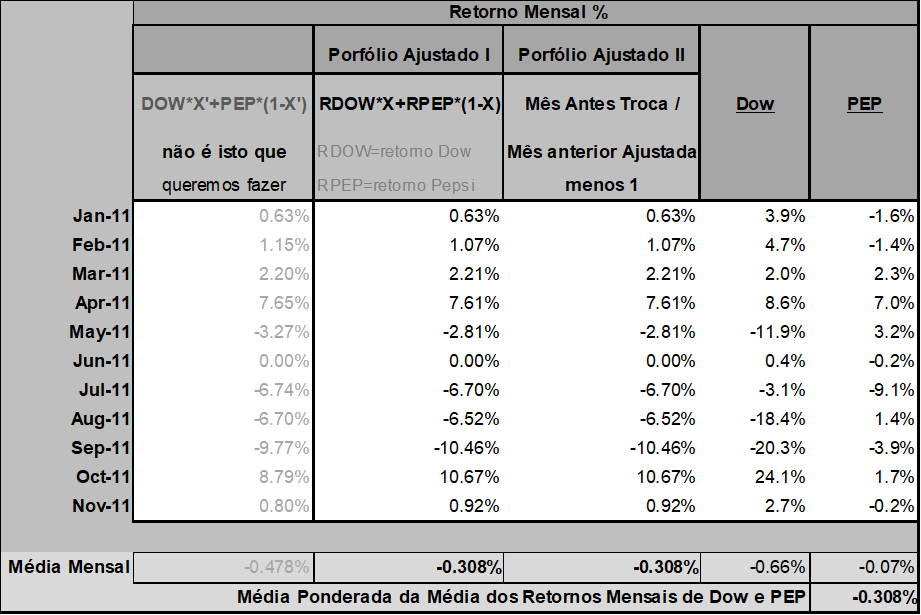
Na segunda coluna “Portfólio Ajustado I” (Figura 23) o retorno médio foi calculado como a média ao longo dos meses do retorno Dow multiplicado pela participação monetária (40%) investido em Dow mais o retorno Pepsi multiplicado pela participação monetária (40%) investido em Pepsi em cada mês. Como exemplo em fevereiro de 2011 temos: 3,9% × 40% + -1,4% × 60% = 1.07%.

Na terceira coluna “Portfólio Ajustado II” o cálculo parte da (Figura 23). Primeiro em cada mês fazemos a divisão do índice do portfólio ajustado antes da troca do mês em vigor pelo índice mês anterior “ajustada” com a venda e compra de ações para ajustar os percentuais do índice. Depois calculamos a média dos resultados em todo o período. Para exemplificar, novamente o cálculo de fevereiro de 2011 fica assim: 47,99 / 47,48 – 1 = 1,07%.

Portanto, ao se formar um portfólio constante de duas ações, mantendo-se, em cada mês, o percentual investido em valores monetários na proporção definida, resulta em se obter um retorno igual à média ponderada das médias de retornos mensais dos dois papéis. Esta afirmação não seria verdadeira se estivéssemos mantendo o número de ações de cada empresa desde uma compra inicial. É necessário que ocorram trocas de ações (compra e venda) para manter em cada mês uma parcela fixa dos investimentos em cada empresa. Somente assim valem as condições estatísticas que estamos querendo demonstrar para um portfólio de duas ações.

Em seguida vamos apresentar a outra variável estatística definidora da curva normal, chamada Covariância. Covariância se define entre uma ação e um portfólio, entre dois portfólios, ou, no exemplo, entre essas duas ações no mesmo período, Dow e Pepsi. Esta variável estatística é uma das medidas de variabilidade do portfólio. Se elas andam juntas, esta variável tende a ser próxima da Variância dos retornos das ações individualmente. Se quando uma sobe a outra desce (o que é muito difícil), então o portfólio das duas ações tende a ter um risco muito menor que cada ação individualmente.

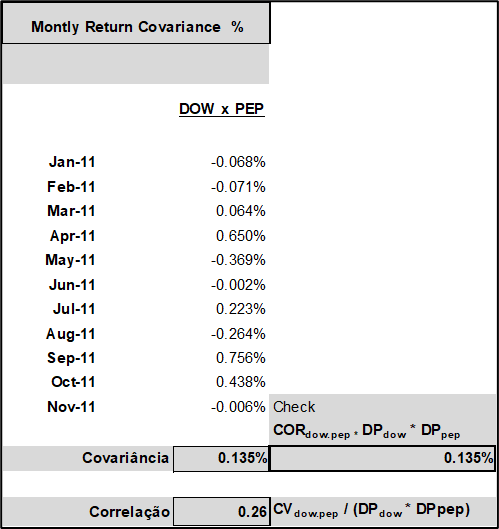
A Covariância é dada pela soma, ao longo dos meses, da multiplicação entre as diferenças entre o retorno mensal de cada ação e o seu retorno médio no período, dividido pelo número de eventos menos um. Matematicamente escrevemos:

Covariância = ∑ [ (retornos mensal ação A – média dos retornos mensais ação A ) × (retornos mensal ação B – média dos retornos mensais ação B) ] / (n^o de eventos – 1)

No exemplo para 2011 das ações Dow e Pepsi, temos o que mostra a (Figura 24).

Agora vamos observar como se comportam a Variância do retorno e, dessa forma, o Desvio Padrão, nesse portfólio de duas ações:

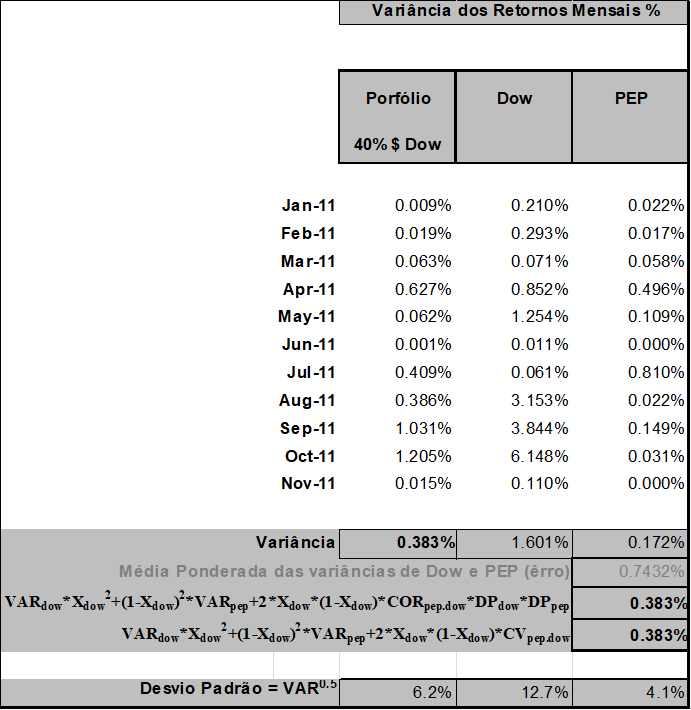
Vamos Demonstrar que a Variância do portfólio é dada pela fórmula: Variância_{Port Pep Dow} = VAR_Dow× X_Dow² + VAR_Pep × (1 -X_Dow)²+ 2 × X_Dow × (1-X_Dow) × CV_Dow.Pep

Definições:

Variância_DOW = ∑[(Ret. Mensal_Dow – média dos Ret. Mensais_Dow)²] / (N^o de meses -1)

Variância_PEP = ∑[(Ret. Mensal_Pep – média dos Ret. Mensais_Pep)²] / (N^o de meses – 1)

Variância_Port = ∑[(Ret. Mensal_Port – média dos Ret. Mensais_Port)²] / (N^o de meses -1)

Mas sabemos que:

Ret. Mensal_Port = Ret. Mensal_Dow × X_Dow+ Ret. Mensal_Pep × (1-X_Dow)

E também que:

Média R. Mensal_Port = média R. Mensal_Dow×X_Dow+ média R. Mensal_Pep×(1 -X_Dow)

Então fazendo as devidas substituições:

Variância_Port = ∑{[R. Mensal_Dow × X_Dow + R. Mensal_Pep× (1-X_Dow) – média dos R. Mensais_Port]²} / (N^o de meses -1)

Variância_Port = ∑{[R. Mensal_Dow × X_Dow + R. Mensal_Pep× (1-X_Dow) – média R. Mensal_Dow×X_Dow – média R. Mensal_Pep×(1 -X_Dow)]²} / (N^o de meses -1)

Variância_Port = ∑{[R. Mensal_Dow × X_dow – média R. Mensal_Dow × X_Dow + R. Mensal_Pep× (1-X_Dow) – média R. Mensal_Pep×(1 -X_Dow)]²} / (N^o de meses -1)

Variância_Port = ∑{[ (R. Mensal_Dow – média R. Mensal_Dow) × X_Dow + (R. Mensal_Pep – média R. Mensal_Pep) × (1 -X_Dow)]²} / (N^o de meses -1)

Variância_Port = ∑{[ (RM_Dow– mRM_Dow) × X_Dow + (RM_Pep– mRM_Pep)×(1 -X_Dow)]²} / (N^o de meses -1)

Variância_Port = ∑{[ (RM_Dow – mRM_Dow) × X_Dow+ (RM_Pep– mRM_Pep)×(1 -X_Dow)]²} / (N^o de meses -1)

Fazendo a multiplicação dos fatores do quadrado: Variância_Port = ∑{[ (RM_Dow – mRM_Dow)²× X_Dow² + (RM_Pep– mRM_Pep)²× (1 -X_Dow)²+ 2 × X_dow × (1-X_dow) × (RM_Dow -mRM_Dow) × (RM_Pep – mRM_Pep) ]} / (N^o de meses -1)

E como a somatória de 3 parcelas é igual a soma das somatórias de cada parcela:

Variância_Port ={ ∑[ (RM_Dow – mRM_Dow)²× X_Dow²] + ∑[(RM_Pep– mRM_Pep)²× (1 -X_Dow)²] + ∑[2 × X_dow × (1-X_dow) × (RM_Dow -mRM_Dow) × (RM_Pep – mRM_Pep)] } / (N^o de meses -1)

Isolando o fator constante de cada somatória (aplicando a propriedade distributiva da multiplicação em relação à adição):

Variância_Port ={ ∑[ (RM_Dow – mRM_Dow)²]× X_Dow² + ∑[(RM_Pep– mRM_Pep)²] × (1 -X_Dow)²+ 2 × X_dow × (1-X_dow) × ∑[(RM_Dow -mRM_Dow) × (RM_Pep– mRM_Pep)] } / (N^o de meses -1)

Chamando “N^o de Meses -1″ de “M” para simplificar:

Variância_Port ={ ∑[ (RM_Dow – mRM_Dow)²]/M× X_Dow² + ∑[(RM_Pep– mRM_Pep)²]/M × (1 -X_Dow)²+ 2 × X_dow × (1-X_dow) × ∑[(RM_Dow-mRM_Dow) × (RM_Pep – mRM_Pep)]/M }

Aplicando as definições de Variância:

Variância_Port = VAR_Dow× X_Dow² + VAR_Pep × (1 -X_Dow)²+ 2 × X_dow × (1-X_dow) × ∑[(RM_Dow – mRM_Dow) × (RM_Pep – mRM_Pep)]/M

Aplicando a propriedade distributiva da multiplicação em relação à adição novamente:

Variância_Port = VAR_Dow× X_Dow² + VAR_Pep × (1 -X_Dow)²+ 2 × X_dow × (1-X_dow) × ∑[(RM_Dow -mRM_Dow) × (RM_Pep– mRM_Pep) / M ]

Reconhecendo que expressão abaixo é a definição de Covariância entre ações Pepsi e Ações Dow no período:

∑[(RM_Dow -mRM_Dow) × (RM_Pep– mRM_Pep) / M ] = CV_dow.pep

Chegamos, finalmente, ao cálculo da formula que define a Variância de um portfólio com X ações Dow e (1-X) ações Pepsi:

Variância_Port = VAR_Dow× X_Dow² + VAR_Pep × (1 -X_Dow)²+ 2 × X_Dow × (1-X_Dow) × CV_Dow.Pep

Conhecidas a origem das variáveis estatísticas dos retornos das ações e a história dos fechamentos mensais ajustados com a distribuição de dividendos, vamos seguir com as consequências da formação de portfólios de ações Dow e Pepsi com variadas composições, agora num longo período, entre janeiro de 1990 e novembro de 2011. Assim foi composta a ().

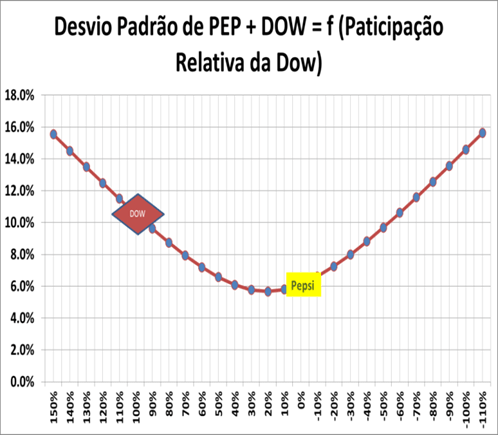
Na (Figura 26) vemos que, como a ação da Dow teve uma rentabilidade no período menor que a ação da Pepsi, à medida que reduzimos seu percentual o retorno aumenta. O interessante é observarmos o comportamento do desvio padrão na (Figura 27), medida da volatilidade ou risco do portfólio, como função da composição relativa do portfólio expresso em % do investimento em ações da Dow.

Se somente tivéssemos ações Dow, teríamos um desvio padrão alto de 10.6% para uma média de retorno de 0.89% ao mês e se tivéssemos somente ações da Pepsi teríamos um desvio padrão de 6.1% ao mês para um retorno de 1.05% (Figura 26). Apesar da ação da Pepsi ter uma tendência de volatilidade menor que a ação da Dow, a combinação delas pode reduzir a volatilidade do portfólio. Note-se que a Variância desse portfólio atingiriam um mínimo próximo de 20% de ações Dow e 80% de ações Pepsi e não somente com ações da Pepsi!

De fato este ponto de mínimo exato pode ser definido pela inflexão da fórmula que deduzimos há pouco. A inflexão da curva do Desvio Padrão do portfólio Pepsi e Dow como função de da participação da Dow é dada pela derivada da equação:

Variância_Port = VAR_Dow× X_Dow² + VAR_Pep × (1 -X_Dow)²+ 2 × X_Dow × (1-X_Dow) × CV_Dow.Pep

Vamos simplificar as notações para calcular a derivada da equação do quadrado do Desvio Padrão, pois na inflexão da Variância, é também estará inflexão da sua raiz quadrada, o Desvio Padrão:

Var_{pep dow} = y = VD.x² + VP + VP.x² – 2.VP.x + 2.CV. x – 2.CV.x²

no mínimo, dy/dx=0; e como d( f(x) +- f’(x) )/dx = d f(x)/dx +- df´(x)/dx então:

0 = d(vd.x²)/dx + d(vp)/dx + d(vp.x²)/dx – d(2.vp.x)/dx +d(2.CV. x)/dx – d(2.CV.x²)/dx

E como d(f(x).A) = A.d(f(x))/dx; d(f(xⁿ)/dx = n.d(f(x)/d(x^n-1) e d(A) = 0 sendo A constante

0 = 2.vd.x + 0 + 2. vp.x – 2.vp + 2.CV – 4.cv.x

2.vd.x + 2 vp.x – 4.cv.x = 2.vp – 2.cv

vd.x + vp.x – 2.cv.x = vp – cv

x.(vd + vp – 2.cv) = vp – cv

x = ( vp – cv) / (vd + vp – 2.cv)

x = 0.25% / 1.25%

x = 20.4%

Variância ou desvio Padrão mínimos ocorreram com um portfólio com 20.4% do montante monetário investidos em ações Dow e com 79,6% em ações Pepsi.

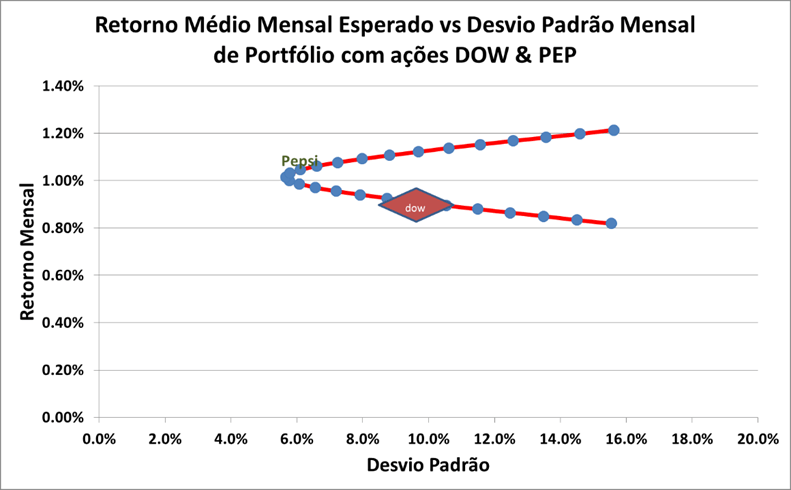
A partir da mesma tabela da (Figura 26) desenhamos a curva da Rentabilidade Mensal versus o Desvio Padrão do portfólio as participações das duas ações (Figura 28). O Menor Desvio Padrão que se pode conseguir com portfólios formados por Dow e Pepsi é 5,67%, com 20.4% de ações Dow e 79,6% de ações Pepsi, como foi calculado pela derivação acima.

DP_dow.pep = ( VAR_Dow× X_Dow² + VAR_Pep × (1 -X_Dow)²+ 2 × X_Dow × (1-X_Dow) × CV_Dow.Pep)^0.5

DP_dow.pep = (1.11× 20.4%² + 0,37% × (1 -20.4%)²+ 2 × 20,4% × (1-20,4%) × 0.12%)^0.5 = 5.67%

Assim, retorno e volatilidade de cada ação definem a demanda média por aquele tipo de ação, e o retorno do portfólio ideal pode sugerir que uma determinada porcentagem de ações com menor retorno e maior desvio ainda podem otimizar esse portfólio. Ou seja, existe demanda para ações relativamente ‘piores’ mas que maximizam o risco x retorno do portfólio como um todo.

Portfólios com múltiplas ações

Tomemos agora um portfólio com grandes números de ações. Como exemplo, usaremos o portfólio das ações que formam o índice Dow Jones que hoje (Novembro de 2011) inclui essas 30 grandes corporações negociadas na bolsa de NY:

Nome Sigla Área de atuação

3M MMM Conglomerado
Alcoa AA Aluminio
American Express AXP Finanças
AT&T T Telecommunicação
Bank of America BAC Banco
Boeing BA Aeronaves e defesa
Caterpillar CAT Construção e equipamentos mineração
Chevron Corporation CVX Petróleo e gas
Cisco Systems CSCO Network de computação
Coca-Cola KO Refrigerantes e bebidas
DuPont DD Química
ExxonMobil XOM Petróleo e Gas
General Electric GE Conglomerado
Hewlett-Packard HPQ Tecnologia
IBM IBM Computadores e technologia
Intel INTC Semicondutores
Johnson & Johnson JNJ Farmacêutica
JPMorgan Chase JPM Banco
Kraft Foods KFT Processamento de alimentos
McDonald’s MCD Fast food
Merck MRK Farmacêutica
Microsoft MSFT Software
Pfizer PFE Farmacêutica
Procter & Gamble PG Bens de consumo
The Home Depot HD Varejo de Material de Construção
Travelers TRV Seguros
United Technologies Co UTX Conglomerado
Verizon Communications VZ Telecomunicação
Wal-Mart WMT Varejo
Walt Disney DIS Radiofusão e entretenimento

Tomemos a curva de distribuição dos retornos versus o número de ocorrências mensais dos retornos, para o portfólio Dow Jones (DJ), entre janeiro de 1980 e novembro de 2011. Vamos compará-las com as curvas que já foram mostradas, relativas às ações individuais Pepsi e Dow. A curva normal do portfólio é mais estreita e elevada que as das ações individuais. Isto significa que há maior concentração de retornos, menor desvio padrão e, portanto menor risco:

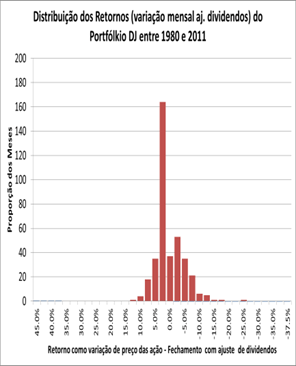
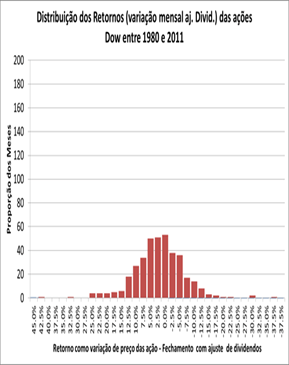
Como já discutimos, a curva normal pode ser completamente definida pelo sua média e pelo seu desvio padrão.

Já provamos que o portfólio de duas ações (ou de uma ação e um portfólio) tem o Retorno Médio dado pela média ponderada dos retornos médios esperado entre eles, podemos ir incluindo mais e mais ações aos portfólios resultantes, de tal forma a obter-se o portfólio final. Por exemplo, o Dow Jones. Assim, o Portfólio de muitas ações tem um Retorno Médio definido pela média ponderada (ponderada pelo montante investido) das médias dos retornos esperados de cada uma das ações. Matematicamente:

Ret_port

…onde x_ié a o a razão do investimento em cada das “n” ações do portfólio sobre todo o investimento e r_i é o retorno médio esperado de cada uma dessas ações.

Já vimos que o Desvio Padrão de duas ações é dado por:

Variância port_{dow, pep} = VAR_Dow× X_Dow² + VAR_Pep × (1 -X_Dow)²+ 2 × X_Dow × (1-X_Dow) × CV_Dow.Pep

Agora que nos acostumamos com as variáveis, vamos passar a utilizar a notação tradicional das mesmas:

Desvio Padrão da ação i = σ_i

Variância da ação i = σ_i²

Covariância entre ação i e ação j = σ_ij

Correlação entre ações i e j = ρ_ij

Retorno médio da ação i = ř_i

A fórmula da covariância já demostrada apresentada fica descrita como segue:

σ_port(i,j)²= σ_i²× x_i² + σ_j²× (1-x_i)² + 2 × x_i × (1 – x_i) × σ_ij

Notem que esta fórmula é igual à “produtoria” dos desvios padrões proporcionais:

Covariância entre n ações =

No caso de n = i,j temos

σ_port(i,j)² = (σ_i×x_i) ×(σ_i×(1-x_i))

σ_port(i,j)² = σ_i²×x_i² + σ_j²× (1-x_i)² + 2 × x_i × (1 – x_i) × σ_i × σ_j

σ_port(i,j)² = σ_i²×x_i² + σ_j²× (1-x_i)² + 2 × x_i × (1 – x_i) × σ_ij

Já que (1 – x_i) = x_j , esta fórmula pode ser decomposta em suas parcelas como na tabela abaixo (Figura 30):

Sendo que: σ_port(i,j)²= Soma dos 4 elementos e, portanto, o desvio padrão do portfólio será dado por: σ_port(i,j)= (Soma dos 4 elementos)^0.5

Caso o portfólio fosse apenas uma ação então x_i=100% e obviamente teríamos que:

σ_port(i,i)= ( σ_i²×x_i²)^0.5 = ( σ_i²×100%²)^0.5 = ( σ_i²×1)^0.5 = ( σ_i²)^0.5 = σ_i

No caso de DJ index temos uma matriz de 30 linhas e 30 colunas, montada semelhantemente, tendo na diagonal a variância de cada empresa, vezes o quadrado da participação de cada uma das 30 empresas e nos outros espaços. Por exemplo, na coluna Alcoa e linha American Express, teríamos a multiplicação:

(x _Alcoa × x _Aexpress× Covariância _{Alcoa,AExpress})

x _Alcoa = participação fixa monetária da Alcoa no índice DJ

x _Aexpress =participação fixa monetária da AExpress no índice DJ

Lembrando que Covariância também pode ser descrita como e a tabela abaixo ter os quadros amarelos descritos em função das correlações e desvios padrões.

σ_{Alcoa,AE =}ρ_Alcoa,AE× σ_{Alcoa ×} σ_AE

Abaixo a grande tabela descrevendo as parcelas da Variância do portfólio Dow Jones a partir das variâncias e covariâncias de cada par de ações entre todas as empresas do portfólio ( note que usei “.” como sinal de multiplicação) :

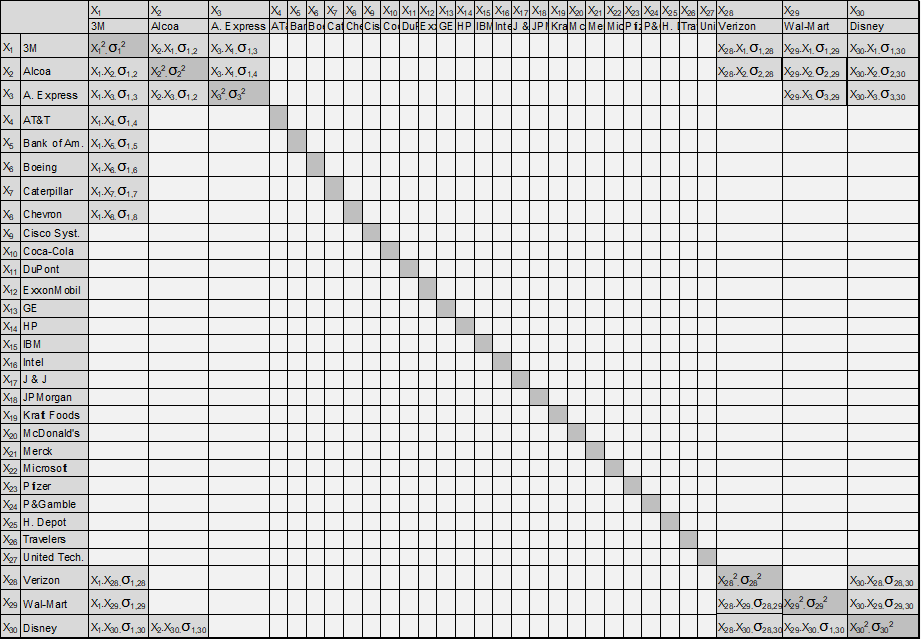
Vamos proceder a uma rápida análise dimensional da (Figura 31). À medida que aumentamos o número de ações no portfólio, a fração x_i diminui, e mais ainda diminui o seu quadrado. O número de parcelas da tabela do portfólio DJ é 30×30 = 900 e, caso os investimentos fossem exatamente iguais, o valor de x=1/30, e seu quadrado seria x²= 1 / 30² = 1 / 900. Assim, se todas as ações se movessem paralelamente, e, portanto, apresentassem covariâncias e variâncias iguais, então o resultado da Variância do Portfólio seria igual à Variância idêntica dos retornos de todas as ações:

σ_Port²= 900 × (1/900 × σ_i²) = σ_i²

O fato de terem comportamentos diferentes é o que produz covariâncias de cada par de ações potencialmente menores que as variâncias de cada ação desse par e, portanto, fazem com que a Variância e o Desvio Padrão do portfólio diminuam, reduzindo seu risco.

Afinal, na tabela existem 30 parcelas que dependem das variâncias de cada ação e 900 – 30 = 870 parcelas que dependem da Covariância de cada par de ações do portfólio.

O limite para a redução do risco está no fato de que, na verdade, todas as ações, em maior ou menor dimensão, estão sujeitas as flutuações do mercado como um todo, e suas Covariâncias não conseguem anular-se. O que se anulam são as flutuações individuais de cada ação por razões internas da empresa, que, por sua origem, não ocorrem concomitantemente nas outras empresas.

Obviamente o leitor mais rigoroso com a lógica percebe que esta demonstração não é academicamente profunda, fui econômico quanto às premissas, definições de mercado ideal e outros detalhes. Entretanto creio que ofereci o suficiente para a compreensão conceitual das bases da definição de custo de capital próprio (equity) a partir das alternativas de investimento em outras empresas e nos portfólios de melhor risco retorno sem aborrecer demasiadamente, assim espero, meu leitor mais prático!

Critério para Apuração do Custo do Capital Próprio

Como vimos, as alternativas de investimento do investidor em ações formam a base da definição do custo do equity da empresa. A empresa necessita estar competitiva do ponto de vista de retorno e risco para atrair investidores quando buscam um aumento de capital através de venda de ações ordinárias da empresa. Uma das formas de aumentar o retorno futuro e consequentemente a demanda é a redução do preço de mercado da ação.

Vimos que o custo do capital próprio é função das alternativas que tem os donos de uma empresa de investir em outras ações disponíveis no mercado, cada qual com seu risco próprio e passível de diluição até certo ponto com diversificação. Essa opção é o que vai definir o custo ou a ganho alternativo de se investir na própria empresa.

Lembramo-nos das várias formas de financiar o capital próprio, mas indicamos que vamos analisar sua avaliação através do financiamento marginal através da emissão de ações ordinárias.

Ao contrário do custo da dívida, que é estabelecido entre o tomador e o banco ou bancos financiadores, o custo do Patrimônio Próprio (ou custo do Equity) decorre dessa capacidade de atrair investidores e das alternativas destes, ajustada ao risco.

Indicamos que os retornos esperados e variabilidade da ação de uma empresa, por razões práticas, podem ser seu comportamento histórico, tomado num período longo. Esta base, assim tomada, pode não ser correta caso tenham ocorrido grandes mudanças na empresa, no mix de seus produtos, mas tende a ser uma base estatística ao menos razoável, se notarmos que certas tendências de comportamento (caso Dow e Pepsi) se não são idênticos, pelo menos são parecidas em diferentes períodos.

Desde ponto em diante tentaremos mostrar como, quanto e porque esse custo de capital próprio é maior que investir em alguma alternativa de muito baixo risco, como aplicar em Letras do Tesouro.

Vamos procurar entender agora os conceitos básicos dos métodos com base estatística de se estimar esse “custo do patrimônio próprio” da empresa.

Riscos Elimináveis e não Elimináveis pela Diversificação

Pense num investimento de R$10.000 em uma única empresa que o investidor não controla.

O que acontecerá com esse dinheiro se essa empresa tiver uma grande explosão em sua maior fábrica, receber uma multa gigantesca por danos ambientais ou perder um contrato muito grande? Também pode acontecer da empresa inventar um produto maravilhoso, descobrir um processo muito mais barato de produzir um bem e patenteá-lo! Será que o investidor está disposto a perder ou ganhar muito dinheiro devido a esses fatos tão aleatórios? Os investidores tendem a se afastar desse tipo de investimento porque esses eventos podem trazer oscilações muito maiores do que o investidor está disposto a suportar.

Como vimos nas discussões estatísticas, investir esses R$10.000 em muitas empresas pode trazer um bom retorno com um risco mais reduzido. Esse tipo de risco, chamados riscos das firmas, é diversificável.

Por outro lado, riscos de mercado, como uma crise econômica na Europa provocando uma resseção mundial, ou um boom no crescimento mundial com o desenvolvimento acelerado de uma grande economia como a chinesa, são riscos que não podem ser eliminados por diversificação porque tendem a afetar todas as empresas paralelamente.

Um portfólio grande de ações apresenta risco muito menor que o risco de um investimento numa única empresa. Um portfólio de empresas farmacêuticas, por outro lado, pode reduzir alguns riscos de cada firma, mas ele pode estar sujeito a alguns riscos típicos do mercado farmacêutico, tipo controle de preços em alguns países, e apresentarem um risco intermediário.

Os investidores em cada tipo de portfólio ou fundo, ou os investidores em empresas individuais, terão que ter, portanto, expectativas diferentes de retorno ou não investiriam nas oportunidades de maior risco, derrubando seus preços.

Com base nesse conceito básico de que risco requer retorno suficiente para atrair investidores, foram desenvolvidos alguns modelos para mensurar numericamente a variável chamada risco, associada aos retornos requeridos.

Como todos os modelos são estatísticos, e a única base de dados disponível é a histórica, esses modelos tem por base o comportamento das ações no passado. Dados passados tentam estabelecer critérios de comportamento para prever o futuro, portanto têm suas falhas. Todos, entretanto, estabelecem um custo de capital maior ao investir em ações que costumam apresentar maior volatilidade, e sempre muito maior que investir em opções de muito menor risco como letras do tesouro nacional.

Sem pretensão de profundidade acadêmica, escolhemos um método de cálculo do custo do capital próprio, o CAPM. Veremos que mesmo com este objetivo bem singelo precisaremos de todo o arcabouço estatístico que desenvolvemos até aqui.

Introdução ao Modelo CAPM

O CAPM (do inglês: Capital Asset Market Model) foi desenvolvido nos anos 60´s pelos economistas William Sharpe, John Lintner e Jack Traynor.

O método utiliza a análise estatística, ou seja, probabilidade de eventos retorno e volatilidade esperada para as ações e dos portfólios diversificados das empresas, como estudamos nos itens anteriores. Embora o método se refira a probabilidades de ocorrências futuras, das tendências dos preços das ações em relação ao mercado como um todo, na prática, a base de cálculo dessas tendências é sua história tomada num longo período, com o objetivo de minimizar as variações dos riscos não elimináveis. Assim quando usamos o método de forma prática, costumamos não levar em consideração os fundamentos de cada empresa na estimativa das probabilidades de preço futuro, nem a dependência entre os eventos (por exemplo, que depois de uma depressão pode haver crescimento). Tratamos cada evento ocorrido como uma possibilidade estatística.

Vamos usar um exemplo para que se vá apresentando, de forma prática, as variáveis estatísticas usadas neste método:

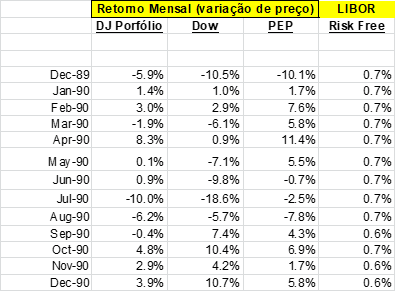
Tomemos o retorno histórico de um portfólio relativamente grande na Bolsa de NY, representado pelo índice Dow Jones (DJ). Iremos assumir que DJ representa bem o mercado todo e assim eliminou todos os riscos diversificáveis. Tomemos também, por exemplo, as ações da Dow Chemical (DOW) e as ações da Pepsi Corporation (PEP). Usaremos os fechamentos mensais ajustados (com a distribuição de dividendos extraídos do site Yahoo Finance) entre janeiro de 1990 e outubro de 2011:

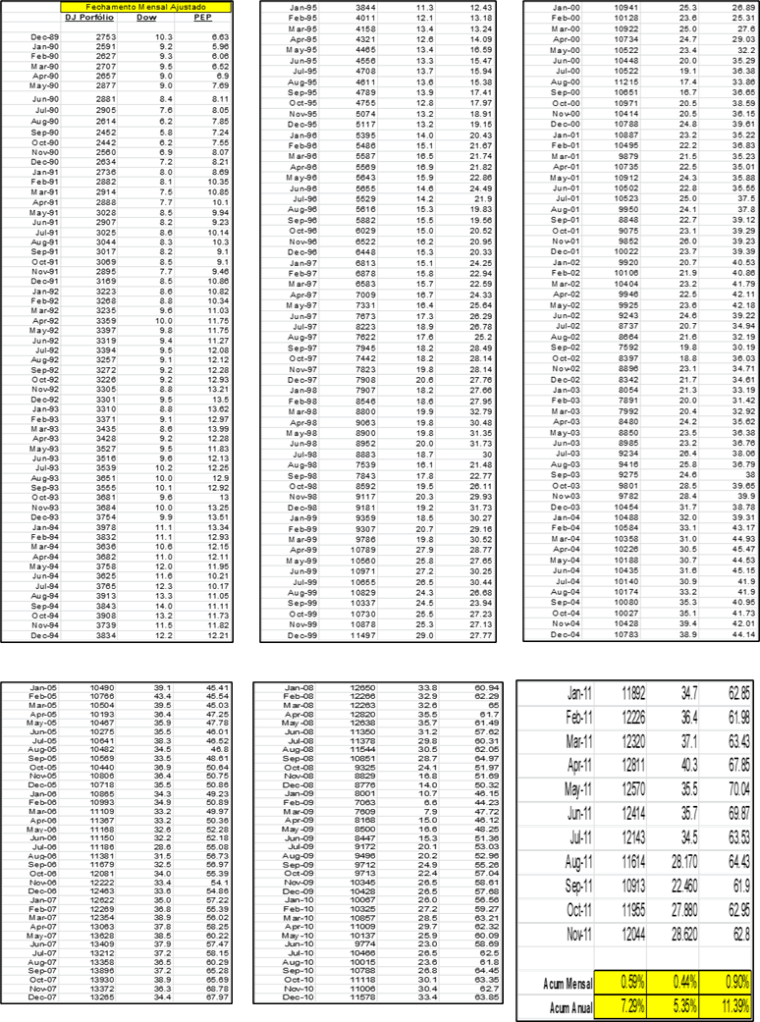
Na amostra histórica da (Figura 32), dividimos o último ponto e primeiro mês da tabela, e extraímos sua raiz (1 / número de meses – 1). Esse retorno de ponta a ponta, calculado em % ao mês, é também apresentado em % ao ano. Verificam-se retornos acumulados de 7,29% aa para DJ; 5.35% aa para a Dow e 11,39% aa para a Pepsi.

Retorno ponta a ponta por mês RPP por mês anualizado

Pepsi 0.90% 11,39%

Dow 0.44% 5,35%

DJ 0.59% 7.34%

A partir da mesma base de dados, podemos desenvolver regressões exponenciais desses fechamentos ajustados com dividendos, abandonando tomar somente o início e o final do valor das ações:

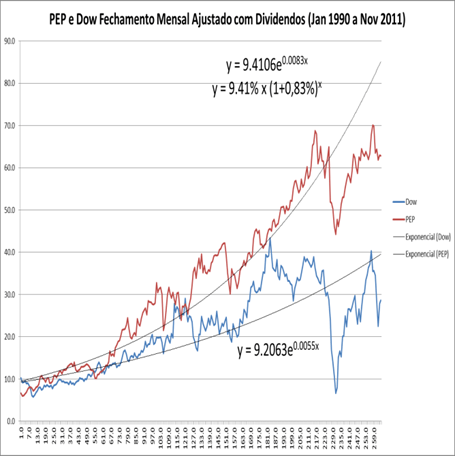
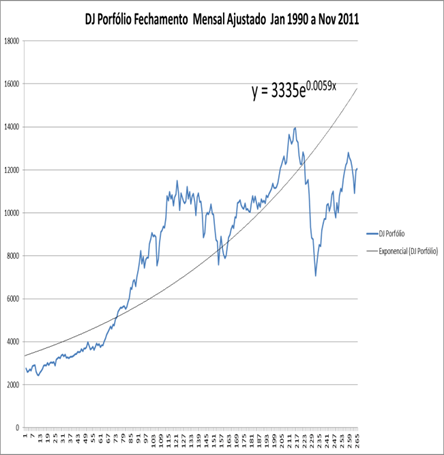
As Fórmulas das Regressões apresentam as seguintes equações (partindo de janeiro de 1990) sendo x o número de meses a partir de janeiro de 1990:

Ação Pepsi: y = 9.4106 × e ^0.0083x ou y = 9.4106 × { 1 + [ (1+0.83%)^x -1 ] }

Ação Dow y = 9.2063 × e ^0.0055xou y = 9.2063 × { 1 + [ (1+0.55%)^x -1 ] }

Portfólio DJ y = 3335 × e ^0.0059x ou y = 3335 × { 1 + [ (1+0.59%)^x -1 ] }

Essas fórmulas implicam em taxas de retorno ou de desconto, aplicáveis de forma composta conforme indicadas a seguir:

CMP mensal CMP mensal anualizado

Pepsi 0.83% 10.47%

Dow 0.55% 6.82%

DJ 0.59% 7.34%

Embora os dois métodos acima representem bem o que ocorreu com as ações da Pepsi e da Dow neste longo período, sabemos que o investidor não está interessado somente no que ocorre individualmente com as ações de cada empresa, porque ele sabe como reduzir pelo menos parte desses riscos estatisticamente. Portanto nãoserão esses os retornos médios utilizadosmétodoCAPM.

O CAPM, métodos de estimativa do custo do capital próprio com base estatística, toma as oportunidades de investir em ações de empresas ao longo do tempo apenas como eventos estatisticamente possíveis em cada período de decisão, não sequenciais. O método considera os vários eventos retorno como variáveis independentes. Dessa forma, numa análise puramente estatística de eventos, calculamos os retornos mês a mês de cada uma dessas séries, bem como a média dos retornos (já mostramos que o retorno médio de um portfólio é igual á média dos retornos).

Na (Figura 34) vemos alguns trechos (iniciais e finais) dos cálculos dessas médias mensais:

===>

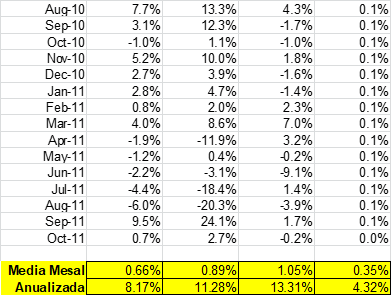
Retorno médio mensal Retorno médio mensal anualizado

Pepsi 1.05% 13.31%

Dow 0.89% 11.28%

DJ 0.66% 8.17%

Libor (Risk Free) 0,35% 4.32%

A média foi calculada como a soma dos retornos mensais dividido pelo número de meses.

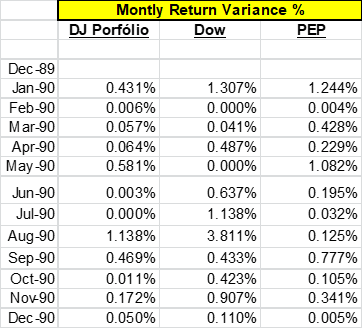
Seguindo-se com a análise estatística dos eventos retorno, a partir da mesma tabela, é possível calcular-se a Variância desses retornos. Variância do Retorno de uma Ação ou Portfólio é a soma dos quadrados das diferenças anuais entre cada retorno periódico e a média dos retornos, divida pelo número de meses menos um. A raiz quadrada da Variância é o Desvio Padrão.

Na (Figura 35) apresentamos início e final da tabela desses cálculos para as ações e portfólio usados no exemplo:

===>

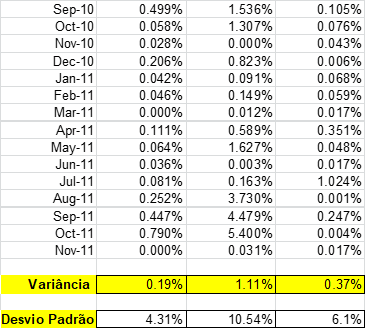
Variância mensal Retorno médio mensal anualizado

Pepsi 1.05% 13.31%

Dow 0.89% 11.28%

DJ 0.66% 8.17%

Libor (Risk Free) 0,35% 4.32%

A seguir calculamos algumas Covariâncias e Correlações duas ações ou entre uma ação e um portfólio. Covariância, como vimos, é a soma do produto das diferenças anuais entre cada retorno anual e a média dos retornos anuais de cada ação, ou de uma ação e um portfólio; divididos pelo número de ocorrências menos um. Vamos novamente mostrar o início e o final da tabela de cálculo de Variâncias, do exemplo, na (Figura 35) :

===>

Fica claro (veja Covariância de DJ x DJ; Covariância = Variância = 0.0019 ou 0.19%) que Variância é um tipo de Covariância da ação ou portfólio com ele mesmo.

Na segunda coluna da tabela apresentamos outra forma de cálculo da Covariância entre os eventos retornos das ações do portfólio Dow e eventos retornos do portfólio Dow Jones. Ele foi feito dividindo-se a soma dos produtos dos retornos mensais da ação DOW pela das diferenças dos retornos anuais do portfólio DJ e a média dos retornos anuais DJ. A média dos retornos da DOW foi desnecessária ao cálculo. Os resultados são idênticos.

Portanto a Covariância pode ser calculada de dois modos:

ρ_ij = [ (r_DJn– ř_DJ) × ([ (r_DOWn– ř_DOW)] / (n^o de eventos – 1)

…ou:

ρ_ij = [ (r_DJn– ř_DJ) × r_DOWn] / (n^o de eventos – 1)

A partir da Covariância podemos calcular a Correlação entre duas ações (ou uma Ação e um Portfólio). Como vimos na revisão estatística, Correlação é o igual à Covariância dessas duas Ações (ou de uma ação e um portólio) dividida pelo produto dos seus Desvios Padrões. No caso da Correlação entre Dow e DJ temos que:

CORRELAÇÃO _DOW.DJ = COVARIÂNCIA_DOW.DJ / ( DP_DOW × DP_DJ)

CORRELAÇÃO _DOW.DJ = 0.0028 / (10.54% × 4.31%) = 60.69% ( não muito alta)

Note que a correlação entre uma ação e ela mesma é 100%, veja:

CORRELAÇÃO _DOW.DOW = COVARIÂNCIA_DOW.DOW / ( DP_DOW × DP_DOW)

CORRELAÇÃO _DOW.DOW = VARIÂNCIA_DOW.DOW / ( DP_DOW × DP_DOW)

CORRELAÇÃO _DOW.DOW = VARIÂNCIA_DOW.DOW / (VARIÂNCIA_DOW.DOW ) =100%

Apresentadas as suas variáveis, voltemos ao método CAPM. O método assume que é possível se diversificar ações ( ou portfólios de investimento com risco) de tal forma que para um determinado Retorno Médio, se forme um portfólio que apresente uma Variância mínima positiva, pois alguns riscos serão não diversificáveis. Ações individuais e outros portfólios com este definido Retorno Médio esperado teriam Variâncias maiores que este portfólio que chamamos de Eficiente do ponto de vista risco e retorno. No gráfico da (Figura 37), os pontos da curva parabólica representam todos esses Portfólios Eficientes onde os investidores preferem estar. Quaisquer outros portfólios com igual retorno estariam horizontalmente à direita dessa curva, portanto com Variâncias maiores e seriam inadequados. Todos os portfólios ineficientes estariam na porção côncava da curva. Obter-se tal curva é um trabalho significativo e complexo. Atinge-se este objetivo por um tipo de programação linear chamada programação quadrática[1]. Se considerarmos as possibilidades, poderemos imaginar essa dificuldade.

O método CAPM então presume a associação desses investimentos com risco que estão na fronteira de eficiência, com variáveis proporções de investimentos sem risco (Risk Free), ou seja, com Variância zero. Essa associação define uma linha reta, conforme mostraremos a seguir. A Variância desses dois portfólios (i=Risk Free e j=Portfólio da Fronteira Eficiente) é assim definida, conforme já mostramos:

σ_port(i,j)²= σ_i²×x_i² + σ_j²× x_j² + 2 × x_i × x_j × σ_ij

Como o Portfólio i não tem risco => σ_i²~ 0; σi=0 e σ_ij = σ_i × σ_j × ρ_ij = 0

Portanto:

σ_port(i,j)²= 0 + σ_j²× x_j² + 0 = σ_j²× x_j²

σ_port(i,j) = σ_j× x_j

Como “σ_j”é uma constante em relação a “x_j” está equação é uma reta do tipo y = c.x , assim concluímos que o Desvio Padrão do portfolio combinado em relação à porcentagem do portfólio de risco “j” é uma função linear do desvio padrão desse portfólio de risco “j”.

O mesmo pode-se dizer do retorno esperado desse portfólio combinado, já que por definição ele é a média ponderada dos portfólios médios de risco e “ risk free”. Veja:

ř_ij = ř_j × x_j + ř_i × (x_j – 1)

ř_ij = ř_j × x_j + ř_i × x_j – ř_i

ř_ij = (ř_j + ř_i) × x_j – ř_i

Como ř_j , ř_i, a equação acima é do tipo y’ = a. x + b que também define uma reta.

Então ao combinarmos as duas equações y’ = a. x + b onde x = y / c, concluímos que y’=f(y) também é uma reta:

y’ = a. (y / c) + b

y’ = a/c . y + b onde a/c e b são constantes em relação a x.

Substituindo-se y’, y, a, b e c por seus parâmetros temos a reta:

ř_ij = (ř_j + ř_i)/ σ_j × x_j – ř_i

A curva do gráfico da (Figura 37) representa a fronteira de eficiência entre risco (variância ou desvio padrão) e retorno de possíveis portfólios formados somente por investimento de risco (aqueles que para cada tipo de retorno oferecem o menor desvio padrão).

Existem muitas retas possíveis dessas combinações, algumas coincidentes como as das combinações do portfólio de risco A e Risk Free e a B e Risk Free. No ponto exato B da combinação do Portfólio B com ações Risk Free (RF) nós teríamos 100% de participação do portfólio B e 0% de RF e, claro, no ponto RF, nós teríamos 100% de ações Risk Free.

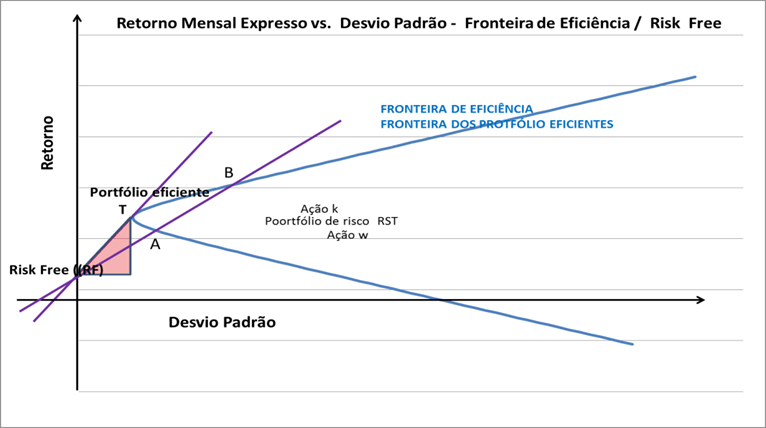
O que significa a inclinação de uma reta em particular que combina investimento Risk Free (RF) e Portfólio T quando comparada com a de qualquer outra reta tipo RF e Portfólio A ou RFe Portfólio B? Significa que nesta reta, por ser a mais inclinada entre todas possíveis, para cada possível Retorno Médio, obtemos o menor Desvio Padrãopossível dentro da fronteira de eficiência que passa pelo retorno Risk Free (Combinações de RF e investimentos eficientes de risco). Assim, esta reta de portfólios mistos entre ações de risco, segundo o portfólio eficiente T, e investimento Risk Free, é o mais eficiente deles ao combinar risco e retorno. Quando existem ações Risk Free, o portfólio T é o que oferece a melhor combinação entre a curva da fronteira de eficiência das ações com risco e investimentos Risk Free. Esta reta (que passa por T e RF) é, portanto, a Reta do Mercado de Capital. Investidores avessos a risco iriam preferir investir na reta com combinações muito próximas a RF para obter o melhor retorno possível com o mínimo de volatilidade (por exemplo, investidores de fundos de aposentados que dependem desse retorno como salário mensal). Aqueles investidores que buscam retornos maiores a prazos mais longos (investidores de fundos de ações e outros investidores com perfil agressivo) buscariam pontos próximos da reta por volta ou até um pouco acima de T.

Assim o mercado todo dos investimentos com risco é esse grande portfólio de ações definindo o ponto “T”. Na prática é comum usar-se alguns portfólios de referência como o SP500 ou DOW JONES (DJ) como sendo esse mercado, ou portfólio T. Então podemos usar a fórmula da reta: Y_T = a. X + b, onde:

Y_T = retorno do portfólio ideal onde;

b = retorno Risk Free;

a = inclinação da reta do gráfico acima (dada pelo cosseno do ângulo da reta com o eixo horizontal que passa pelos pontos com coordenadas (0,Risk Free) e (Desvio Padrão_DJ, Retorno_DJ).

Portanto “a” pode ser definido como o cosseno do ângulo esquerdo do triângulo retângulo da (Figura 37):

a = (Retorno_DJ – Risk Free) / (Desvio Padrão_DJ)

Assim a equação da reta “Y_T = a. X + b” passa a ser:

Retorno_DJ = [ (Retorno_DJ – Risk Free) / (Desvio Padrão_DJ) ] × Desvio Padrão_DJ+ Risk Free

Retorno_DJ = Risk Free + (Desvio Padrão_DJ/Desvio Padrão_DJ) × [ (Retorno_DJ – Risk Free)]

Se chamarmos a inclinação da reta (Desvio Padrão_DJ/Desvio Padrão_DJ) de β_DJ (beta do índice Dow Jones):

Retorno_DJ = risk free + β_DJ × (Retorno _DJ – risk free) …onde β_DJé igual a 1, já que o estamos definindo com relação a este portfólio eficiente que se confunde com o mercado.

Historicamente entre os anos de 1990 e 2011, independentemente dos valores iniciais e finais, tivemos que Risk Free (baseado na taxa Libor na (Figura 37), mas poderia ser um Título Público) foi em média 4.32% aa enquanto que o Índice DJ rendeu 10,54% aa e que o Desvio Padrão _DJ no período foi de 4.31%. Assim, com dados em eventos por uma longa história, assumidos como eventos esperados no futuro, fica descrita as relações de risco e retorno do portfólio ideal de risco:

r_DJ = risk free rate + β_DJ × (Prêmio por risco) = risk free rate + β_DJ × (6.21%)

A seguir vamos explorar algumas consequências do uso dessa Reta do Mercado de Capital.

Efeito Redutor do Risco ao combinar Ações

Ao combinarmos duas ou mais ações, é possível provocar um efeito estatístico de atenuação da volatilidade. Vejamos o efeito de montar portfólios de ações Dow e Pepsi, onde X_dow é a participação percentual de ações Dow no portfólio, e , obviamente, (1-X_dow) é a participação das ações da Pepsi.

Desvio Padão do Portfólio DOW e PEP = ρ_portfólio

ρ_portfólio= (ρ_dow²× X_dow² + (1-X_dow)²× ρ_pep² + 2 × X_dow×(1-X_dow) × ρ_pep.dow × ρ_dow× ρ_pep )^0.5

Se usarmos os dados históricos entre janeiro de 1990 e novembro de 2011, teremos o gráfico já discutido no resumo estatístico.

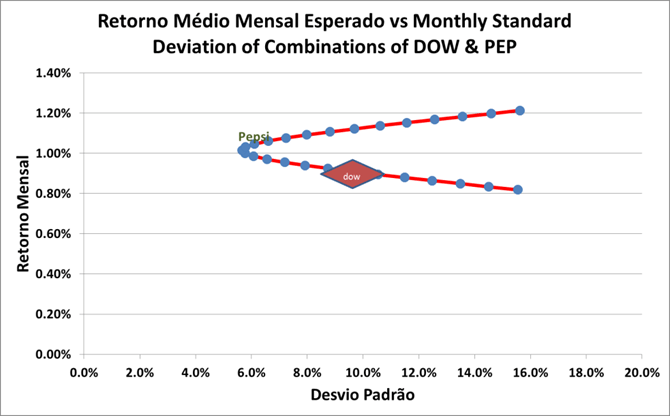
A curva de todos os portfólios formados por ações Dow e Pepsi apresenta alguns desvios padrões que são inferiores tanto ao Desvio Padrão dos retornos das ações Dow quanto aos das ações Pepsi.

Para um portfólio maior esse efeito redutor continua acontecendo com o limite estabelecido pelos riscos de mercado que implicam em efeitos semelhantes a todos as ações e que, portanto, não podem ser eliminados.

Retorno Esperado de uma Determinada Ação

Um investidor eficiente somente investirá em uma única ação se ela estiver na reta do Mercado de Capital (adequando risco e retorno). Se tomarmos qualquer ação individualmente ao longo do tempo, é possível se estabelecer sua relação com o retorno do portfólio de risco ideal (assumido como DJ) e a taxa Risk Free. Se tomarmos os retornos das ações Dow de janeiro de 1990 e novembro de 2011 teremos:

Retorno esperado do Portfólio ideal = risk free + βdow × (Retorno DJ – risk free)

Custo do Equity Dow = risk free + βdow × (Retorno DJ – risk free)

Ou seja, para atrair capital para a Dow Chemical, seus projetos devem precisam remunerar a taxa sem risco (risk free ~ Libor, Letras do Tesouro) mais a diferença entre o retorno esperado num portfólio ideal (assumimos DJ) multiplicado pelo fator de risco relativo das ações da Dow contra as ações do portfólio.

Onde β_dow pode ser estimado de diversas maneiras:

(1) Cálculo do Beta (β) pela fórmula com dados da (Figura 39) e (Figura 40): βdow = cov(dow,dj) / var(dj) = 0.2758% / 0.1858% = 1.484

βpep = cov(pep,dj) / var(dj) = 0.1329% / 0.1858% = 0.715

(2) Beta’s também podem ser estimados com base geométrica, ou seja, com base na fórmula gráfica da equação linear da dispersão relativa dos retornos das ações da Dow contra os retornos do portfólio Dow Jones:

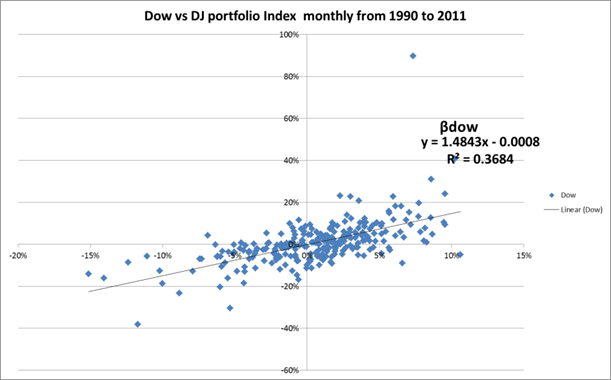
Neste caso o β_dow seria igual ao coeficiente da dispersão entre os retornos mensais anualizados da Dow versus os do Portfólio assumido ideal: ou seja β = 1,4843.

Assim o custo do Equity para a Dow seria:

Cost of Equity DOW = risk free+ βdow × (Return DJ – risk free)

Custo do Equity DOW = 4.32%+ 1,4843 × (8,17% – 4,32%) = 10,03%

O investidor menos avesso a risco investirá em ações Dow se pelo menos puder esperar um retorno de 10.03%.

E de forma semelhante para a Pepsi:

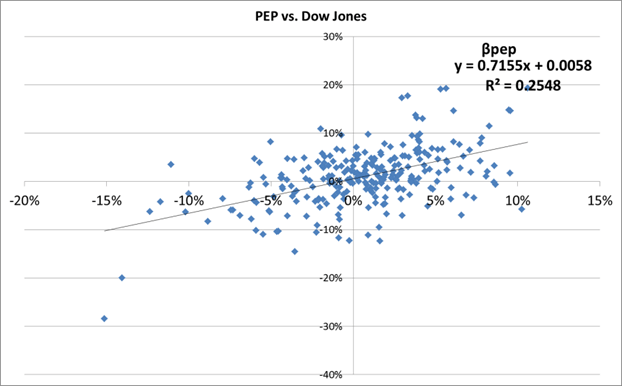
…ou seja β = 0,7155.

E o custo do Equity para a Pepsi seria:

Cost of Equity_PEP= risk free+ β_pep × (Return DJ – risk free) =

Cost of Equity _PEP= 4.32% + 0.7155 × (8.17% – 4.32%) = 7.07%

Já para o Portfólio de referência teríamos o seguinte:

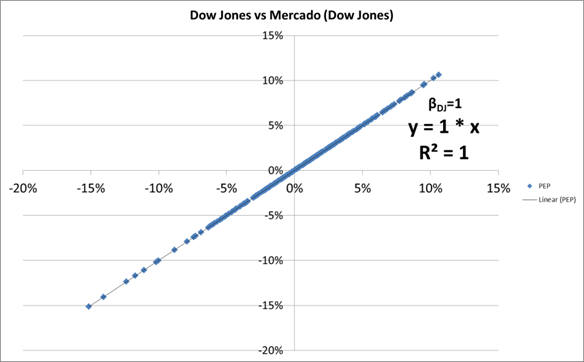
Obviamente um β = 1, por definição.

E o custo do Equity para a DJ seria:

Cost of Equity _DJ = risk free+ β_DJ × (Return_DJ – risk free) =

Cost of Equity_DJ= 4.32% + 1 × (8.17% – 4.32%) = 8.17% pois é a referência e o portfólio no ponto tangencial reta com a curva de portfólios eficientes quanto a risco e retorno.

Assim, ações que tem alta correlação tem covariância muito próxima da variância de cada uma e não formam um bom conjunto no portfólio que objetiva reduzir risco (Variância), isto é, formam um portfólio provavelmente distante da linha fronteira de eficiência que mostramos no gráfico logo abaixo.

Outro aspecto que observamos é que certas ações tem alguma tendência de movimento contrário ao mercado. Uma das ações que analisamos (Pepsi) tem este tipo de comportamento. Por esse motivo o β da Pepsi é menor que uma unidade. Um β menor que a unidade faz com que o retorno equivalente necessário para os projetos dessa empresa possa ser menor que o retorno esperado para o próprio mercado.

Assim, apesar de não detalharmos o desenvolvimento teórico do modelo (de estimativa do custo do capital próprio CAPM) indicamos os parâmetros básicos do seu conceito e dos seus principais cálculos.

Breves insights da teoria de Modigliani e Miller

Modigliani e Miller (MM) apresentaram um teorema em 1958 de que numa economia competitiva, livre de imposto, de custos de falência e com decisões lógicas e uniformes dos investidores, as estruturas de capital seriam irrelevantes ao valor da empresa. O que vamos fazer a seguir é mostrar os principais insights resultantes dessa teoria:

A teoria estabelece que, dado o valor presente de um fluxo de caixa definindo o valor de um ativo real, o fato de dividi-lo em partes não altera seu valor. Assim deixando o ativo real com investimento alavancado ou não, não altera seu valor.

Se por exemplo, num país sem impostos, um indivíduo é dono de 100% das ações de uma empresa e de 100% da dívida da empresa, este indivíduo é dono da empresa. Assim, supondo que não haja impostos, caso ele decida alterar a estrutura de capital da empresa, diminuindo dívida e aumentando capital próprio, o valor da empresa não pode ser alterado pois o valor depende da capacidade da empresa gerar fluxo de caixa ou retorno. Assim o Custo de Capital da Empresa (= r _{ativos reais} = r _{Portfólio de Divida e Equity )} não pode ser alterado.

Suponha que esta firma tenha 60% em equity e 40% em dívida e que o retorno esperado do equity seja de 20% e o custo da dívida de 10%

Assim r _{ativos reais} = D/V × r _D + E/V × r _E

r _{ativos reais} = 40% × 10% + 60% × 20% = 4% + 12% = 16%

Se esta empresa tem um projeto de aumentar seu próprio negócio e decida que este investimento será feito com capital próprio, o retorno esperado da empresa r_{ativos reais} não muda, mas como a empresa agora está menos alavancada ela oferece menor risco. Então suponha que a empresa passa a ter70% de capital próprio e 30% de dívida, o que deve acontecer com o custo do equity, caso o custo da dívida, pelo menor endividamento caia para 8%?

r _{ativos reais} = 30% × 8% + 70% × r _E = 2.4% + 70% × r _E = 16% => r _E = 13.6% / 70% = 19.4%

Assim, embora o retorno esperado da firma não mude, tanto o retorno esperado do seu equity quanto o da sua dívida caem.

Vamos ver o que acontece com o risco da empresa no caso de mudança na estrutura de capital. Numa empresa há riscos, e embora o risco do equity seja muito maior que o risco da dívida, existe algum risco nesta dívida. Novamente, se

r _{ativos reais} = RF + β_{ativos reais} × (r_DJ – RF)

r_E = RF + β_E × (r_DJ – RF)

r_D = RF + β_D × (r_DJ – RF)

Como r_{ativos reais}permanece inalterado o que mudam são r_E e r_D

r _{ativos reais} = D / (D + E) × r _D+ E / (D + E) × r _E

r _{ativos reais} = D / (D + E) × [RF + β_D × (r_DJ – RF)]+ E / (D + E) × [RF + β_E × (r_DJ – RF)]

onde (r_DJ – RF) = MP = Market Premium over Risk Free e D+E = Value (V)

r _{ativos reais} = D / V × [RF + β_D × MP] + E / V × [RF + β_E × MP]

r _{ativos reais} × V = D × RF + D × β_D × MP + E × RF + E × β_E × MP

r _{ativos reais} × V = (D + E) × RF + D × β_D × MP + E × β_E × MP

r _{ativos reais} × V =V × RF + D × β_D × MP + E × β_E × MP

r _{ativos reais} = RF + D/V × β_D × MP + E/V × β_E × MP

r _{ativos reais} = RF + ( D/V × β_D + E/V × β_E ) × MP

β_{ativos reais} = D/V × β_D + E/V × β_E

Dessa forma, supondo que RF =8% e MP = 6% temos que:

r _{ativos reais} = RF + β_{ativos reais} × (r_DJ – RF) = 16%

r _{ativos reais} = 8% + β_{ativos reais} × 6% = 16%

β_{ativos reais} = 8% / 6% = 1.33

E antes do projeto teríamos:

r_D = 8% + β_D × 6% = 10%

β_D = 2%/6% = 0.333

Seguindo-se no mesmo caso acima antes do projeto:

β_{ativos reais} = 40% × 0.333 + 60% × β_E = 1.33

β_E = (1.333 – 0,13333)/60% = 2.0

ou de outra forma:

r_E = RF + β_E × (r_DJ – RF) = 20%

8% + β_E × 6% = 20%

β_E = 12%/6% = 2.0

Calculemos agora o impacto nos ricos com o investimento no projeto:

RF =8% e MP = 6% obviamente são os mesmos:

Assim como os retorno e risco da empresa.

β_{ativos reais} = 1.33

Mas o retorno esperado da dívida mudou r_D = 8% + β_D × 6% = 8% e consequentemente seu risco

β_D = 0%/6% = 0

e para o equity:

r_E = RF + β_E × (r_DJ – RF) = 19,4%

8% + β_E × 6% = 19,4%

β_E = 11,6%/6% = 1.9333

Isto é, tanto o retorno quanto o risco da dívida e do equity caíram pelo fato da Dívida sobre o Valor ter caído, mas como o peso do equity no valor aumentou, nada mudou no real asset (a empresa).

Num extremo, com 100% de ativo, tanto os retornos quanto os riscos do equity se reduziriam até se confundir com os do asset.

No outro extremo, a firma 100% endividada teria um custo da dívida igual ao retorno esperado da firma e o risco da dívida subiria até confundir-se com o risco da firma.

Assim, num economia ideal e sem impostos, a estrutura de capital não deve afetar o retorno ou o risco da empresa.

Métodos de cálculo do custo de capital da Empresa (WAAC e APV)

Uma empresa num mundo com riscos requer alguns ajustes nas fórmulas derivadas das propostas de Modigliane e Miller.

r _{ativos reais} = D / (D + E) × r _D + E / (D + E) × r _E …ou

r _{ativos reais} = D / V × r_D + E / V × r_E … com ativos reais sendo fixo qualquer seja D/V ou E/V

passa a ser:

WACC = D / V × r _D × (1 – TAX) + E / V × r _E …com WACC < r _{ativos reais}

Em outras palavras, temos uma taxa de desconto da empresa potencialmente variável e diferente do custo de oportunidade da empresa ( r _{ativos reais} ).

Assim, o uso da derivação do WACC a partir de dados estatísticos, pressupõe a manutenção da estrutura de capital similar às que geraram os dados. A indiferença proposta por MM já não mais se sustenta. Assim o método WACC, embora sendo o mais usado pelos analistas, nos traz essas limitações e, pode provocar erros importantes se for usado fora das suas limitações. O WACC tem que ser usado dentro de uma determinada e fixa estrutura de capital.

Como alternativa a este método, existe o método APV (Adjusted Present Value), que não resolve o problema da estrutura rígida de capital, mas que, por ser mais didático, pode evitar que se cometam os erros típicos de quem se utiliza do WACC sem o devido conhecimento de suas limitações:

O método APV propõe que se avalie um projeto de uma empresa como se ele fosse totalmente desalavancado, ou seja, como se ele fosse totalmente financiado por equity.

Em seguida adicionam-se as vantagens fiscais por haver possibilidade de financiá-lo, caso seu risco seja semelhante ao risco da empresa, ao nível da alavancagem da empresa.

Sumarizando os métodos para avaliar um projeto ou uma firma:

WACC aplica a seguinte metodologia:

Estime o fluxo de caixa alavancado do Projeto ou Firma.
Calcule o Valor Presente (PV) do fluxo de caixa usando uma taxa de desconto ajustada ao risco, o qual varia com o grau de endividamento que atribuamos ao projeto.

APV use a seguinte metodologia:

Estime o fluxo de caixa desalavancado do Projeto ou Firma.
Use quaisquer métodos para calcular o Valor Presente do Projeto ou Firma como se a firma fosse financiada apenas com capital próprio (equity).
Adicione o valor do Escudo Fiscal (Tax Shield) associado ao financiamento via dívida, pois o pagamento da dívida faz com que haja um imposto menor que no projeto desalavancado.

Em ambos os métodos, além das dificuldades de se compreender os fluxos de caixa do projeto, existe esta dificuldade primordial de se definir as taxas de desconto e risco.

Lembrando-se que equity é sempre definido como o valor de mercado das ações, não o valor de livro que é apenas uma ilustração contábil dessa variável.

O analista financeiro que pretende utilizar o método WACC (ou o APV) precisa entender como os impostos alteram os vários componentes do balanço da firma valorizado a mercado em termos de taxa de retorno esperado e risco.

Um balanço para esse fim, mas sem impostos seria assim:

Ativos	Passivos
	Dívida = D
Ativos = D + E	Equity = E

Figura 42

Um balanço para esse fim, mas com impostos seria assim, sendo T_rate = Taxa de imposto efetiva da corporação, sendo que TX é o valor presente das reduções de impostos devidos à existência de dívida:

Ativos	Passivos
Escudo Fiscal (TX) = TX	Dívida = D
Ativos Desalavancados (AD) = D + E – TX	Equity = E

Figura 43

Quando apresentamos as ideias de Modigliani e Miller no item anterior, mostramos que o valor da firma é o valor da firma desalavancado.

r _{ativos reais} = D / (D + E) × r_D + E / (D + E) × r_E

β_{ativos reais} = D / (D + E) × β_D + E / (D + E) × β_E

… e como normalmente β_E é muito pequeno, se aproximando de Risk Free (β = 0) para a mairoia dos Blue Chips, podemos aproximar essa equação de:

β_{ativos reais} = E / (D + E) × β_E

…que ao isolarmos o Beta do equity se transforma em:

β_E = ( 1 + D / E) × β_{ativos reais}

…lembrando que D+E=V (valor real não contábil).

Vamos assumir, nesta empresa, um imposto estável, da forma TX = D × T_rate,sendo T_rateuma constante.

O retorno esperado (WACC) da empresa alavancada pode ser menor que o retorno do capital próprio mais o retorno da dívida, devido ao escudo fiscal.

WAAC = D / (D + E) × r_D + E / (D + E) × r_E – (D × T_rate) / (D + E) × r_D

WAAC = E / (D + E) × r_E + (D – D × T_rate) / (D + E) × r_D

WAAC = E / (D + E) × r_E + (1 – T_rate) × D / (D + E) × r_D

WAAC = w_E× r_E + w_D × (1 – T_rate) × r_D…onde w_E= % de equity e w_D = % de dívida.

Do ponto de vista de risco temos:

β_fima= AD / (D + E) × β_AD + TX / (D + E) × β_TX

E como em função do beta da dívida, e também do escudo da taxa ser quase nulo:

β_{ativos reais} = E / (D + E) × β_E …e: TX / (D + E) × β _TX ~ 0

Temos:

E / (D + E) × β_E = AD / (D + E) × β_AD + TX / (D + E) × β _TX … que simplificada produz:

E / (D + E) × β_E = AD / (D + E) × β_AD + 0

E × β_E = AD × β _AD … e substituindo o valor de AD

E × β_E = (E + D – D × T_rate) × β _AD

β_E = [1 + (1 – T_rate) × D / E] × β_AD

Estas equações têm algumas consequências muito importantes. Como o Beta da empresa não alavancada (β_AD ) não varia com a alavancagem (dívida versus capital total) ou com o imposto, então, se tomarmos um determinado endividamento (D/E = constante) o Beta do equity aumenta conforme o imposto diminui, e chega a seu máximo quando o imposto é zero. Também o Beta do equity aumenta com o aumento da dívida.

Assim, a equação “WAAC = w_E× r_E + w_D × (1 – T_rate) × r_D”quando aplicada em projetos, precisa manter no projeto o mesmo endividamento e taxa de impostos usados na empresa, pois alterações nesses parâmetros alterariam sobremaneira o WACC por alterarem o β_Ee, consequentemente, o r_E esperado.

Sem dúvida o método WACC é o mais utilizado na vida prática. Entretanto na bibliografia consultada, pareceu-me unanimidade a preferência pelo método APV (Adjusted Present Value) do ponto de vista acadêmico. A razão para esta preferência prática distinta da acadêmica me parece ser bem simples. Numa grande empresa, como as multinacionais, ao aplicar-se o WACC, o cálculo do custo de capital é deixado para um grupo mais sênior de Financistas e os demais analistas apenas se preocupam com a correta avaliação dos fluxos de caixa sem alavancagem financeira. Algumas dessas empresas tentam atribuir certas diferenciações nas taxas de desconto do capital, classificando-as quanto ao risco derivados dos negócios ou das geografias, enquanto outras empresas definem um taxa única que passa a ser o balizamento para se aprovar ou rejeitar um projeto do ponto de vista financeiro. O método APV pode simplificar a discussão teórica sobre taxa alavancada e sendo teoricamente mais elegante. Entretanto a facilidade se aplicar uma metodologia uniforme em toda empresa, é razão suficiente para o contínuo sucesso do método WACC.

Vamos a um exemplo de cálculo de custo de capital:

Exemplo de Cálculo do WACC

Cálculo do WACC da The Dow Chemical Company

Em primeiro lugar é preciso se identificar algumas variáveis financeiras da empresa (dados extraídos de informações públicas disponibilizadas aos acionistas):

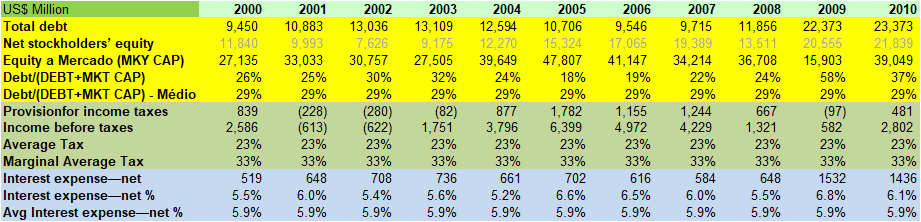
A alavancagem típica da Dow é de aproximadamente 30% de Dívida sobre o Capital total a mercado.

Embora, neste período, a média de impostos sobre lucro tenha sido de 23%, por ser uma empresa americana sua taxa de imposto de renda marginal deve estar por volta de 33%.

O custo do Equity da Dow já foi calculamos nas explicações do método CAPM:

Cost of Equity _DOW = risk free+ β_dow× (Return_DJ – risk free)

Taxa Esperada para Equity _DOW = 4.32%+ 1,4843 × (8,17% – 4,32%) ~10,0%

Como a Dow é uma empresa BBB ela consegue levantar recursos de longo prazo um pouco acima do custo risk free (RF+2), o que daria algo em torno de 6 % aa em 2011. No ano do cálculo (2011) as taxa de curto prazo estiveram menores, mas as de longo prazo permaneceram no patamar indicado.

WAAC = w_E× r_E + w_D × (1 – T_rate) × r_D

WAAC_DOW= 70%× 10.0% + 30% × (1 – 33%) × 6% = 8,2%

Assim, definidos os princípios teóricos das metodologias de cálculo e utilização do custo de capital passaremos a sua utilização como ferramenta de avaliação econômica.

Posted on

WAGNER RODRIGUES POETA E CRONISTA