WAGNER RODRIGUES POETA E CRONISTA

Continuação de texto inédito

Taxa nominal como artifício para desconto de fluxos contínuos constantes

Primeiramente devemos definir fluxo uniforme e fluxo contínuo de caixa. Até este momento tratamos de fluxos discretos que ocorrem no final de cada período. Na prática da empresa os fluxos de caixa não são discretos do ponto de vista anual (talvez sejam discretos a nível diário). Basicamente também não são uniformes. Entretanto, principalmente no planejamento de mais longo prazo, assumi-los contínuo, isto é, ocorrendo uniformemente durante cada ano e divididos em infinitos períodos durante um ano, aproxima-se bastante dos resultados de valorização a nível diário. Claro que imaginar um fluxo discreto no meio do ano também não prejudica muito a qualidade da análise para um projeto de vários anos de duração. Mas o fluxo contínuo será mais próximo da realidade.

A matemática que desenvolveremos a seguir pode ser um pouco complicada na sua demonstração, mas proporciona uma modelagem simples ao analista. A planilha de um fluxo de caixa diário feita para 10 anos teria mais de 3500 períodos e esgotaria o número de colunas do Excel. Com o uso da matemática que veremos a seguir, a planilha pode conter apenas 10 períodos anuais e ainda assim representar fluxos próximos aos diários, desde que uniformemente distribuídos dentro de cada período. Frequentemente essa uniformidade durante o ano é uma hipótese razoável para a vida futura da empresa ou negócio, ao menos para planejamento.

Considerar um fluxo contínuo significa dividir o fluxo monetário de caixa anual (montante simplesmente somado de dinheiro no período) em infinitas parcelas uniformes, seja para se fazer o cálculo do valor presente, ou para identificar a uma eventual taxa interna de retorno decorrente de um investimento inicial.

O principal artifício que se usa nesta matemática é a definição de Taxa Nominal Contínua de Desconto (ou de Juros).

Taxa Nominal (chamaremos de TN’) pode ser definida a partir da taxa real  (r) da seguinte forma:   TN’ anual capitalizada a cada um de n períodos é tal que (1 + TN’ / n)ⁿ – 1 = r,

ou seja, se n = 2 períodos, dada uma taxa nominal TN’=10%, sua taxa real correspondente seria calculada dessa forma:

[(1 + 10% / 2)² – 1] = r = 10.25%;

se n = 4 períodos dentro de um ano, uma taxa nominal de 10% capitalizada trimestralmente seria:

[(1 + 10% / 4)⁴ – 1] = r = 10.3812891%; e assim por diante.

Demonstrações rumo à Taxa Nominal Contínua

Se formos aumentando o número de subdivisões do período a ponto de que o mesmo vá tendendo ao infinito, nós estaremos definindo a taxa nominal contínua, que chamaremos simplesmente de TN.

A relação desta TN com a taxa anual “r” real seria tal que: [(1 + TN / n)ⁿ – 1] = r, com o número de subdivisões (n) dentro do ano tendendo ao infinito.

Matematicamente, essa relação é descrita como: r = lim_n>∞ [(1 + TN / n)ⁿ  ] – 1 (podemos colocar “-1” fora do limite já que é independente de “n”.

Em seguida demonstraremos que essa expressão “lim_n->∞ [(1 + x / n)ⁿ  ]” é uma das formas de se definir e^x (usando x  no lugar de TN, representando uma variável qualquer).

É bem divertido trabalhar-se com essa matemática, já que ela está ligada à trigonometria parabólica, base matemática para as transformadas de Lorenz, matemática fundamental para a Teoria da Relatividade de Einstein.

Para provar o que queremos, temos duas demonstrações a fazer:

• Demonstrar que d/dx (e^x )= e^x
• Demonstrar que e^x = lim_n>∞[(1 + x / n) ⁿ]

Primeira Demonstração: Prova de que d/dx (e^x )= e^x

Por definição de derivada de uma função f(x) = x dizemos que:

d/dx x =  lim _h->0 {  [ (x + h) – (x) ] / h}.  

Portanto a derivada da função f(x) = e^x  analogamente será:

d/dx e^x = lim _h->0  {[e^{x + h}  –  e^x] / h} = lim _h->0  [e^x × (e^h – 1) / h].

Mas como e^x  é uma constante em relação à variável “h”, seu limite em relação a qualquer valor de “h” é ela mesma. Assim a própria função e^x pode ser posta em evidência fora do limite relativo à variável “h”:

d/dx e^x = e^x . lim _h->0   [(e^h – 1)/h]  (para terminar a demonstração de que d/dx (e^x )= e^x precisamos imaginar que existe algum valor para “e”  tal que o limite que compõem a igualdade acima, que multiplica o fator e^x , tenha uma convergência para a unidade).

De fato, para o neperiano e=2,718281828459045… o lim _h->0  [(e^h – 1)/h]  converge a 1 e, portanto para este valor de e, d/dx e^x = e^x .

A determinação do valor do número neperiano “e” pode ser feita de forma geométrica.

Vamos lá:

Comecemos num ponto específico (x=0). Pela definição de derivada, temos que:

d/dx e⁰ = e⁰ . lim _h>0   (e^h – 1)/h = 1 . lim _h>0  [( e^h – 1)/h] = lim _h>0   [(e^h – 1)/h]

Se na expressão d/dx e^x = e^x . [lim _h>0   (e^h – 1)/h] substituirmos o fator [lim _h>0   e^h – 1]/h  por d/dx e⁰, teremos: d/dx e^x = e^x . d/dx e⁰

Portanto, geometricamente d(e⁰)/dx é a tangente da função y=e^x no ponto onde x=0 e y=1 (pois neste ponto  y = e⁰ = 1).

Então, para x=o, o número “e” é tal que a função y=e^x tem sua tangente y=1. Assim ao usarmos a equação d/dx e^x = e^x . d/dx e⁰ no ponto onde x=0 teremos:

 y = d/dx e⁰ = 1. [lim _h>0   e^h – 1] / h = 1.

Assim, para valores muito pequenos de “h” teremos:

(e^h -1)/h ~ 1 => e^h – 1 ~ h =extraindo a raiz h=> e = (1 + h) ^1/h.

Portanto podemos definir “e” como:

e = lim_h>0 [(1 + h) ^1/h].

Se chamarmos h = 1  / n podemos escrever que: e=lim_n>∞[(1 + 1 / n) ⁿ] e testar a convergência de “e” como mostrado na tabela:

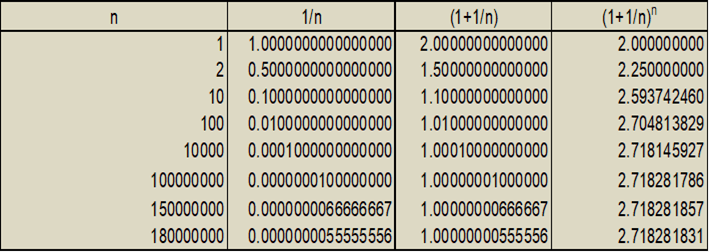
Observamos que existe uma convergência de “e” quando “h” tende a zero ou quando “n=1/h” tende a infinito. Esta convergência define o valor do número neperiano ”e”, um número irracional que vale aproximadamente 2,718281828… 

Portanto, para um número e = 2,718281828…, d/dx e^x = e^x × d/dx e⁰,sendo este segundo fator d/dx e⁰ a tangente de y = e^x com x = 0 e, assim, onde y = 1, estabelecendo que:

d/dx (e^x) = e^x  × 1 => d/dx e^x = e^x

No apêndice ao final do livro, ofereço uma demonstração mais elegante dessa igualdade.

Segunda Demonstração: Prova de que e^x = lim_n>∞[(1 + x / n) ⁿ]

Nessa demonstração testaremos se a expressão é verdadeira para vários valores de “x”:

Assumindo x=0 temos que e⁰ = lim_n>∞[(1 + 0 / n) ⁿ] => 1 = lim_n>∞[(1) ⁿ] => 1= lim_n>∞[(1)] => 1 = 1  => verdadeira

Assumindo que  x=1 e¹ = lim_n>∞[(1 + 1 / n) ⁿ] => verdade como demostrado durante a Parte I acima

Assumindo-se x=2 => e² = lim_n>∞[(1 + 2 / n) ⁿ] =>  e = lim_n>∞[(1 + 2 / n) ^{n / 2}] que pode ser provado por consecutivos aumentos de “n” (Figura 8) como fizemos na Parte I:

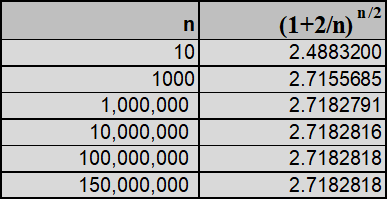
De forma similar tratamos outros valores de x. Por exemplo, x=5 (Figura 9 ) =>

 e⁵ = lim_n>∞[(1 + 5 / n) ⁿ] =>  e = lim_n>∞[(1 + 5 / n) ^{n / 5}]

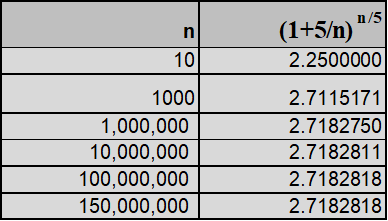
E assim por diante procedemos para vários valores de  x e sempre encontramos que a expressão e^x = lim_n>∞[(1 + x / n) ⁿ] é verdadeira. Claro que há maneiras mais elegantes de se demonstrar, via teoremas, que  e^x = lim_n>∞[(1 + x / n) ⁿ, mas a prova já nos basta.

Recomendo cuidado ao se utilizar da planilha Excel para esses cálculos. É necessário lembrar-se que existe um limite de algarismos significativos com que o Excel trabalha. Dependendo do cálculo sendo feito, se ultrapassado este limite, erros significativos podem ser gerados.

Taxa Nominal Continua

Feitas as demonstrações ou comprovações podemos retomar o início desse capítulo onde tínhamos a definição de taxa real a partir do limite da taxa nominal com períodos “n” tendendo ao infinito:

r = lim_n>∞ [(1 + TN / n) ^{n ]} – 1          

Ao combiná-la com a equação demonstrada na Parte II acima, ou seja, com a expressão

e^x  = lim_n>∞[(1 + x / n) ⁿ] e onde x seria TN, conseguimos:

r = e^TN – 1

Assim fica definida a relação entre taxa anual real e taxa nominal contínua, sendo “e” o número irracional neperiano 2,718281828459045…

A simples inversão da ordem da igualdade oferece a fórmula: eTN = (1 + r) que implica pela definição de logaritmo em: TN = ln(1 + r), i.e. temos a relação entre taxa nominal e função taxa

real de juros. 

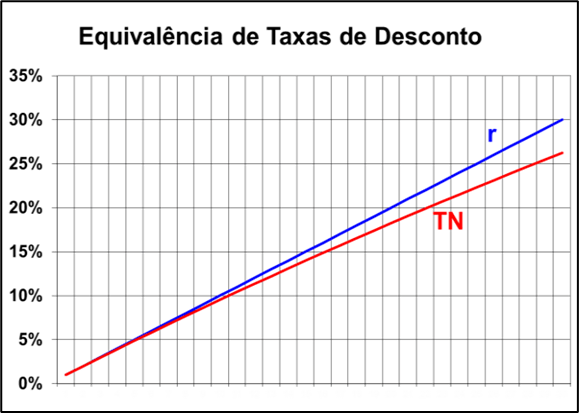
A (Figura 10) mostra um gráfico da relação entre “TN” e “r”. Essa taxa nominal é um poderoso artifício na modelagem de fluxos contínuos com a utilização de fluxos de caixa médios dos períodos. Mostraremos a utilização deste artifício um pouco mais adiante.

Cálculo do valor presente de um fluxo contínuo perpétuo

Para uma anuidade de infinitos períodos e discreta de valor “A” que ocorre ao final de cada ano, já provamos que: PV=A/r. Analogamente será que poderemos dizer que PV=A/TN? Vejamos:

Se essa anuidade  de infinitas parcelas de valor A, ao invés de ocorrer ao final de cada ano, ocorrer semestralmente, podemos escrever:

PV=(A / 2)/[(1 + r)^1/2 -1]

Se continuarmos a subdividir a ocorrência do valor monetário “A” em períodos menores, dividindo o ano, genericamente, em n parcelas, teríamos que:

PV=(A / n)/[(1 + r)^{1 / n}  – 1] ou ainda que: PV=A × {1 / {[(1 + r)^{1 / n}  – 1] × n}}

Agora se levarmos a divisão dos períodos até que n => ∞, com o objetivo de definir um fluxo de caixa contínuo, teremos:

PV = A . lim_n=>∞{1 / {[(1 + r)^{1 / n}  – 1] × n};  (caso tal função convirja a um valor de “r”)

Substituindo-se “r” na equação acima pela sua correspondente taxa nominal “TN” (lembrando-se que r = e^TN – 1) teremos:

PV = A . lim_n=>∞ {1 / {[(1 + e^TN – 1) ^{1 / n}  – 1] × n}  ou

PV = A . lim_n=>∞ {1 / {[ e^{TN / n}  – 1] × n}   (caso tal função convirja a um valor de “r”)

Vamos checar se ocorre esta convergência para diversos valores de “ r” e “TN” à medida que aumentamos o número de subdivisões “n” do período:

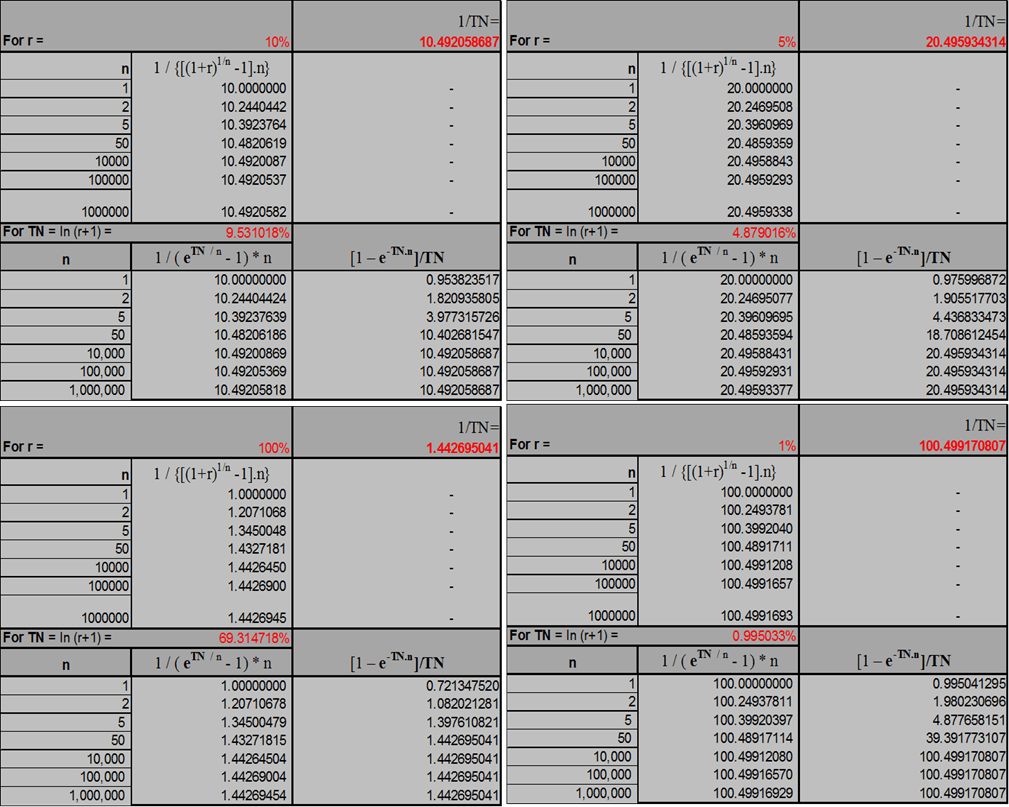
De fato, as tabelas da (Figura 12) mostram que as duas fórmulas de valor presente de perpetuidades de anuidades iguais e contínuas durante todos os anos, independentemente do valor de “r”,  existem e convergem para 1/TN.

Assim, PV = A × lim_n>∞ {1 / {[ e^{TN / n}  – 1] × n}   = A × (1 / TN) = A / TN

Então se considerarmos uma anuidade “A” ocorrendo em cada ano de forma contínua durante infinitos anos (perpetuidade) resulta em um valor presente PV finito e que pode ser calculado por:

PV = A / TN No próximo item demonstraremos como calcular o valor presente de um fluxo anual contínuo utilizando essa definição de perpetuidade contínua.  

De fato, as tabelas da (Figura 12) mostram que as duas fórmulas de valor presente de perpetuidades de anuidades iguais e contínuas durante todos os anos, independentemente do valor de “r”,  existem e convergem para 1/TN.

Assim, PV = A × lim_n>∞ {1 / {[ e^{TN / n}  – 1] × n}   = A × (1 / TN) = A / TN

Então se considerarmos uma anuidade “A” ocorrendo em cada ano de forma contínua durante infinitos anos (perpetuidade) resulta em um valor presente PV finito e que pode ser calculado por:

PV = A / TN

No próximo item demonstraremos como calcular o valor presente de um fluxo anual contínuo utilizando essa definição de perpetuidade contínua.  

Descontando Fluxos de Caixa Contínuos até determinada data.

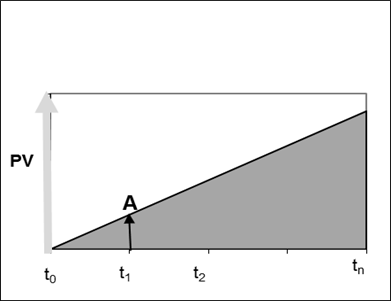
Para calcular o valor presente de um fluxo monetário que ocorre continuamente desde a data zero até uma data n, nos devemos começar calculando o valor presente de duas perpetuidades de anuidades monetárias “A” que ocorrem continuamente durante cada ano, utilizando as fórmulas provadas no item anterior nos momentos t₀ e t_n:

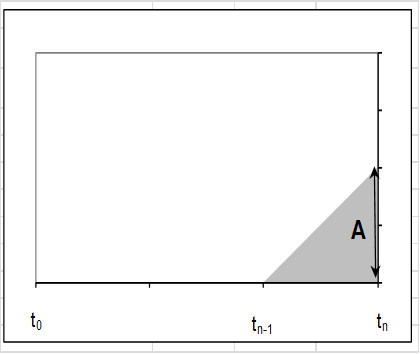
PV_t0 = A/TN (I)    e        PV_tn = A/TN (II)

Mas sabendo que PV_tn é também FV_tn e que este pode ser descontado para PV_t0 temos:  

PV _t0 = FV t_n  / e^{TN × n}  = (A / TN) / e^{TN × n} (III)

Para encontrar o valor presente do fluxo contínuo ocorrido até o ano n basta fazer a diferença entre a equação (I) e a equação (II transformada para III). Assim o valor presente do fluxo contínuo de anuidade “A” ocorrido até o ano “n” é dado por:

PV_t0 = A / TN – A / TN / e^{r × TN}

PV_t0 = A / TN – A × e ^{rTN ×  n} / TN, portanto: PVt₀ = A × (1 –  e^{-TN × n} ) / TN  

E ao combinarmos com a relação entre PV e FV (FV_tn = PVt₀  ×  e^{TN × n}  )

FVt_n =  PVt₀  ×  e^{TN × n}  = [A × (1 –  e-TN × n ) / TN] ×  e^{TN × n}    

FVt_n =  PVt₀  ×  e^{TN × n}  = [A / TN] × (1 –  e^{-TN × n} ) ×  e^{TN × n}    

FVt_n =  PVt₀  ×  e^{TN × n} , portanto:  FVt_n = A × (e^{TN × n}   –  1 ) / TN   (IV)

Caso n seja apenas um ano temos que o valor de um fluxo contínuo uma anuidade A que ocorre continuamente durante o não é dado por:

PV= A × (1 –  e^-TN ) / TN

E a partir dessa fórmula podemos definir também o FV desse fluxo anual continuo de anuidade monetária “A” substituído na fórmula acima que transforma PV em FV para um ano  FV = PV ×  e^TN. Assim teremos:

FV= PV ×  e^TN  = [A  × (1 –  e^-TN ) / TN] × e^TN = A  × [e^TN × (1 –  e^-TN )] / TN FV= A  × (e^TN – 1) / TN

Exemplos

Exemplo 1:

Assumindo o empréstimo de $100 (PV) no início do ano e pagando-se no final do ano $100 mais $10 (r = 10%) como remuneração desse empréstimo, calcular esse valor futuro no final do ano de $110 utilizando tanto a fórmula com taxa de juros discreta de fluxos discretos como as fórmulas de juros de juros contínuos.

1. O próprio texto define o valor futuro: PV($100) + juros pagos no final do ano (10$) = FV($110)
2. Podemos calcular esse valor utilizando a fórmula de juros discretos:                      FV = PV × (1 + r)ⁿ, ou FV = 100 × (1 + 10%)¹ => FV = 100 × 1.10 = $110.
3. Podemos calcular esse valor utilizando a fórmula de juros contínuos, mas para isto precisaremos antes converter a taxa de desconto ou de juros reais para a taxa de desconto ou de juros nominal contínua:                                                                   TN = ln(1 + r) => TN = ln(1 + 10%) => TN = 9.531018.                                     Em seguida podemos aplicar a equação de juros contínuos:                                  PVt₀ = FVt_n  / e^{TN × n} ; mas como n=1 podemos escrever:                                              FV = PV × e^{TN × 1}  => FV=100 × [2.71828 ^9.531018…%] = $110

Exemplo 2:

Imagine um fluxo de caixa contínuo de valor monetário $100 que ocorre apenas durante o 10º ano. Qual o valor presente desse fluxo a uma taxa real de 9.531018%.

1. A fórmula de calculo de uma única anuidade contínua futura e dada por:     PV_t0 = A  × (e^TN – 1) / (TN × e^{TN × n} )
2. As variáveis são: A = $100; n = 10; r = 10,517069% portanto TN = ln(9.531018% + 1) = 10%
3. Então: PV_t0 = $100  × (e^10% – 1) / (10% × e^{10%× 10} ) = $38,69

Exemplo 3:

Imagine um fluxo anual contínuo de 10 anos com anuidades iguais de valor monetário de $100. Qual o valor presente desse fluxo a uma taxa real de 9.531018%.

1. Nesse caso a fórmula para calculo de um fluxo de caixa contínuo de valor monetário anual de $100 é dada por: PVt₀ = A × (1 –  e^{-TN × n} ) / TN
2. As variáveis são: A = $100; n = 10; r = 10,5178069% portanto TN = ln(9.531018% + 1) = 10%
3. Então: PVt₀ = 100 × (1 –  e^{-10% × 10} ) / 10% = $ 632.12

Sumário das fórmulas de matemática da avaliação econômica da apuração da criação de valor

Definição de taxa real de desconto a partir da taxa nominal:  r = e^TN – 1

Definição de taxa nominal a partir da taxa real de desconto:  TN =  ln(1 + r)

Fórmula relacionando PV e FV com taxa nominal:  PV_t0  =  FVt_n  / e^{TN  × n}  

Fórmula relacionando FV e PV com taxa nominal:  FVt_n = PV_t0 × e^{TN  × n}  

Valor presente de uma perpetuidade A contínua: PV_t0 = A/TN

Valor presente de anuidades e iguais contínuas até  o ano “n”: PVt₀ = A ×(1 –  e^{-TN × n} ) /TN

Valor futuro de anuidades iguais e contínuas até  o ano “n”: FVt_n =  A × (e^{TN × n}   –  1 ) / TN 

Valor presente (t₀)  da anuid. A contínua do ano “n”: PV_t0 = A  × (e^TN – 1) / (TN × e^{TN × n} )

Valor futuro da an. A contínua no ano “n”: FVt_n = A × e^TN  × (e^TN – 1) / (TN × e^{TN × n} )

Valor Monetário Anual  A no ano n= f(PVt₀): A = PV_t0  ×  TN /  (1 –  e^{-TN × n} )

Valor Monetário Anual  A no ano n= f(FVtn): A = FVt_n  / e^{TN  × n} ×  TN /  (1 –  e^{-TN × n} )

   A = FVt_n ×  TN / (  (1 –  e^{-TN × n} ) × e^{TN  × n}  )

   A = FVt_n ×  TN /  (e^{TN  × n}   –  1)