continua texto inédito

Descontos de Fluxos Discretos (Matemática Financeira Básica)
Grande parte das projeções de projetos ou até de uma empresa podem ser simplificados em fluxos discretos anuais. A matemática financeira associada é fundamental para quem quer ser um Avaliador Econômico. Mas o que são esses fluxos discretos?
Fluxos discretos de Caixa são fluxos que ocorrem instantaneamente, muitas vezes periodicamente entre intervalos regulares, como todo final de mês, de trimestre ou de ano. Um exemplo seria o de uma pessoa que dispõe de uma poupança e a compra de um televisor pretendido. Tente calcular qual entre duas alternativas é a melhor:
(A) Tirar $1000 de sua poupança, evitando as prestações de uma compra a prazo (por exemplo, em 10 parcelas de $105) ou…
(B) Deixar seu dinheiro na poupança, que paga juros de 0.5% ao mês, já livre de imposto de renda e para pagar as prestações essa pessoa irá retirar da poupança, paulatinamente, o necessário para pagar as prestações.
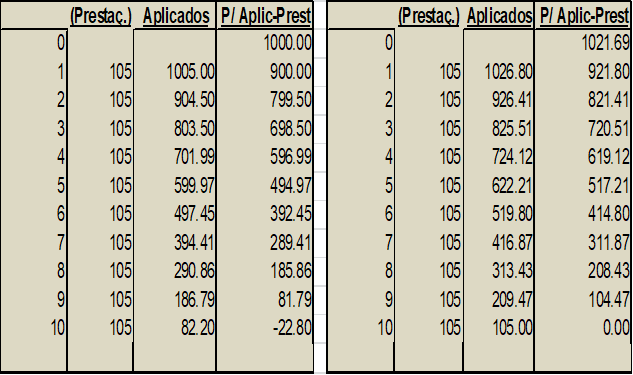
Nas tabelas da (Figura 1) seguem dois tipos de cálculos relativos à opção B. Cada um dos quadros parte de valores iniciais diferentes.
No primeiro quadro partimos do montante que seria da poupança ($1000) equivalente ao valor necessário pagar à vista (que seria a opção A). Mantendo o investimento na poupança e sacando-se o necessário para ir pagando as prestações, mesmo com o rendimento da poupança do que resta investido, no final ficamos devendo $22,80 (Upa! Mau sinal para a alternativa B!).
Na segunda tabela mostramos que para não ficar devendo teríamos que partir de uma poupança maior, de $1021,69 (o valor exatamente necessário, para, como mostrado, ir tirando paulatinamente da aplicação para quitar as prestações).
A resposta fica clara, nas condições apresentadas é melhor retirar da poupança (Alternativa A) e pagar à vista!
Explicando as tabelas: A primeira coluna indica o momento zero da compra e os momentos de pagamento de cada prestação (portanto de zero a 10). A segunda coluna tem os valores das prestações a serem pagas em cada um dos momentos. A terceira coluna tem o resultado do montante que fica acumulado na poupança em cada momento, já com os juros da aplicação, mas antes de pagar a prestação devida naquele momento, portanto disponíveis para pagamentos das prestações em cada período. A quarta é a mesma coisa, depois de pagar as prestações, ou o que sobra aplicado na poupança para os pagamentos futuros. Vejam que o montante da terceira coluna é igual ao montante do mês imediatamente anterior da quarta coluna mais os juros de poupança de 0.5% ao mês.
Na primeira tabela mostramos que, se partimos do valor da TV à vista, faltará $22,80 para pagar a última parcela. Como se mostra na segunda tabela, em valores de hoje, o comprador precisaria aplicar $1021,69 para garantir que teria dinheiro suficiente para pagar as parcelas. Assim, mesmo sem as fórmulas da matemática financeira, sabemos a resposta: Considerando-se as alternativas disponíveis, pagar à vista é melhor que financiar a compra, e o valor da decisão, na data da compra, é de $21,69.
No cálculo acima as variáveis básicas foram fluxos discretos de caixa e taxa de atratividade ou de juros (representando a alternativa do dono do recurso).
No caso, a taxa de atratividade foi definida como sendo os juros pagos mensalmente pela aplicação da poupança, já descontados impostos, e informados como sendo 0.5% ao mês. Esses juros pagos são incorporados ao montante investido de tal forma que passam a ser remunerados da mesma forma que o investimento original assim que completem cada mês. Em matemática financeira esse efeito cumulativo é denominado dejuros compostos, porque não são pagos como cupons, mas reinvestidos.
Um fluxo de caixa discreto do exemplo ilustrado na ( Figura 2) é definido como sendo:
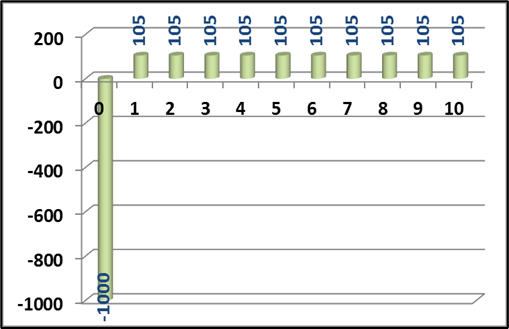
Figura 2
- Uma saída de $1000 (que foi tirado da poupança)…
- … e a partir do mês seguinte 10 entradas iguais e consecutivas de $105 (que são as prestações que foram evitadas).
Convido o leitor a fazer uma pausa para um dos aspectos fundamentais da Avaliação Econômica:
Esse aspecto faz toda diferença na qualidade do aconselhamento. Trata-se do fato de que o avaliador necessita entender a ou as alternativas possíveis de uma tomada de decisão. Na maioria das situações, entender as alternativas possíveis na tomada de decisão não é tão fácil quanto a apresentada neste exercício. De fato, mesmo nesse exercício, nós poderíamos explorar se a poupança é realmente a alternativa melhor possível para quem quer investir os $1000. Ou seja, é fundamental que o avaliador entenda a situação e o negócio da empresa e dos seus donos em profundidade. Sem isto, as técnicas matemáticas não estarão, realmente, maximizando o valor do negócio ou da empresa para seus donos ou acionistas.
Voltando ao exercício:
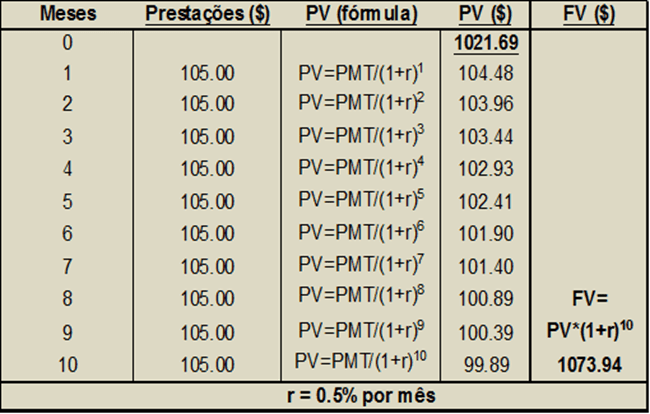
Figura 3
Se um investimento (PV) é investido durante “n” períodos a uma taxa de juros “r” por período, a fórmula de cálculo do valor final (FV) a ser pago com juros é dado por:
FVtn = PVt0 × (1 + r )n ; assim $1000 investidos a 0.5% ao mês acumularão no final do primeiro mês $1005 ( $1005 = $1000 × (1 + 0.5%)1 ); e ao final do segundo mês os mesmos $1000 iniciais já terão rendido $1010,03 ( $1010,03 = $1005 × (1 + 0.5%)1 ou$1010,03 = $1000 × (1 + 0.5%)1 × (1 + 0.5%)1 = $1000 × (1 + 0.5%)2 que demonstra a fórmula acima). Se aplicarmos a fórmula acima, o valor futuro final (no ano “n”) desse investimento “PV” a esta taxa “r” seria: FVtn = PVt0 × (1 + r )n ou FVt10 = $1000 × (1 + 0.5%)10 = $1051.14
Já se tivéssemos uma série de prestações iguais e discretas, como as 10 prestações de $105, conforme mostrado na (Figura 3), e reconhecendo-se a taxa de 0.5% ao mês (nossa taxa de atratividade ou juros da opção que temos), nós teríamos valores como o descrito na figura 3. Essas prestações seriam equivalentes a um valor presente de $1021,69, superior em $21,69 aos $1000 que custa a TV à vista. Na terceira coluna seguem fórmulas de cálculo do valor presente de cada parcela, e na quarta coluna seus resultados. Os $1021,69, são as somas desses valores presentes de cada uma e todas as prestações, ou seja, 2,169% maior que o pagamento à vista. Esse valor presente na data zero de $1021,69 produz um valor futuro na data t=10 de FVtn = PVt0 × (1 + r )n ou FVt10 = $1021,69 × (1 + 0.5%)10 = $1073,94. Novamente, o valor no momento t=10 da $1073.94 é 2,169% maior que os $1051,14, valor futuro no mesmo momento t=10 do pagamento à vista. A proporcionalidade da vantagem de uma alternativa se mantém em cada momento de cálculo financeiro, seja na data t=zero, data t=10 ou quaisquer outros momentos. Esta é uma propriedade fundamental da matemática financeira.
Como deve ter percebido o leitor, devido a origem americana da empresa onde trabalheri toda a minha vida, acabei adotando a nomenclatura em inglês. PV é o valor presente (Presente Value) e assim por diante. Isto também me ajuda a facilitar a tradução para o inglês. Quase todas as pessoas formadas em países do mundo falma inglês, mas poucos falam português, não é?
Séries uniformes discretas e perpetuidades
O que você prefere: ter o direito de ganhar $3000 ao mês durante toda a eternidade, eternidade infinita mesmo, ou ganhar $500000 agora? Você verá que a eternidade não vale tanto quanto parece!
A partir desta questão, vamos ampliar nossas fórmulas da matemática financeira.
Se partirmos de um valor presente de $1000 e desejarmos calcular “n” prestações iguais (chamaremos de P) definidas pela taxa de atratividade (ou juros) de r=0.5% como seria esse cálculo?
Com o objetivo de apresentar outras equações importantes, vamos calcular primeiramente qual o valor presente de uma anuidade perpétua “P” a uma taxa de atratividade “r”. Sim, existe um valor finito e definido na data de hoje, que corresponde a um fluxo estável que irá ocorrer para sempre. Sabemos que o “para sempre” como ato humano não existe. Mas, em matemática, o infinito existe, e, veremos que em matemática financeira, o muito longo e o infinito valem quase a mesma coisa. Veremos que, para taxas usuais de mercado, esse muito longo, é muito longo apenas como uma parcela significativa de uma vida humana! Isto não é de surpreender, pois os rendimentos são pretendidos por indivíduos.
O valor presente (PV) de uma perpetuidade (P) descontada a uma taxa de atratividade “r” pode ser descrita através da seguinte série:
PV = P / (1 + r)1 + P / (1 + r)2 + P / (1 + r)3 + … até o infinito.
Se chamarmos 1 /( 1 + r) = x e chamarmos P /(1 + r) = a, nós podemos reescrever que:
Primeira igualdade: PV = a . (1 + x + x2 + x3 + x4 +….)
Agora se multiplicarmos ambos os termos por x teremos:
Segunda igualdade: PV . x = a . x (1 + x + x2 + x3 + x4 +….)= a . (x + x2 + x3 + x4 +….)
E se agora subtrairmos as duas igualdades anteriores, teremos:
PV – PV . x = a . (1 + x + x2 + x3 + x4 +….) – a . (x + x2 + x3 + x4 +….) ou
PV – PV . x = a . (1) + a × (x + x2 + x3 + x4 +….) – a . (x + x2 + x3 + x4 +….)
Portanto temos que PV . (1 – x) = a . 1
Passemos agora a substituir adequadamente “x” e “a” por suas fórmulas de definição. Assim teremos:
PV . (1 – 1 / (1 + r)) = P / (1 + r)
Se agora multiplicarmos ambos os termos da igualdade por (1 + r) teremos:
PV . (1 + r) × (1 – 1 / (1 + r)) = (1 + r) × P / (1 + r)
PV . ((1 + r) – (1 + r) / (1 + r)) = P
PV . ((1 + r) – 1) = P
PV . r = P
PV = P / r (Viram! A eternidade não vale tanto assim… para uma taxa de 1% ao mês, infinitas parcelas mensais de $3000 valem $300000. Para valer infinitamente a taxa de desconto teria que ser zero.)
Portanto, depois dessas massagens algébricas, mostramos que o valor presente de uma perpetuidade (P) é dado pela divisão dessa perpetuidade pela taxa de atratividade (ou de juros) por período dessa perpetuidade.
Agora fica mais fácil calcularmos o valor presente de 10 parcelas iguais como diferença de duas perpetuidades: Uma delas calculada como PV de infinitas parcelas iguais calculadas na data zero (n=0); e a outra como o PV de infinitas parcelas iguais calculadas na data 10 (n=10). Esta última se torna um FV na data 10 que pode ser calculado como PV na data zero:
Valor presente de uma perpetuidade na data t0 : PVt0 = P / r
Valor presente de uma perpetuidade na data t10 : PVt10 = P / r = FVt10 que pode ser levada a valor presente na data t0 : PVt0 = FVt10 / ( 1 + r)10 = P / r / (1 + r)10;
Subtraindo-se o valor da perpetuidade desde a data t10 e desde a data t0 teremos o valor presente das 10 parcelas iguais:
PV= (P / r) – P / r /(1 + r)10
PV= (P / r) × ( 1 – 1 / (1 + r)10 )
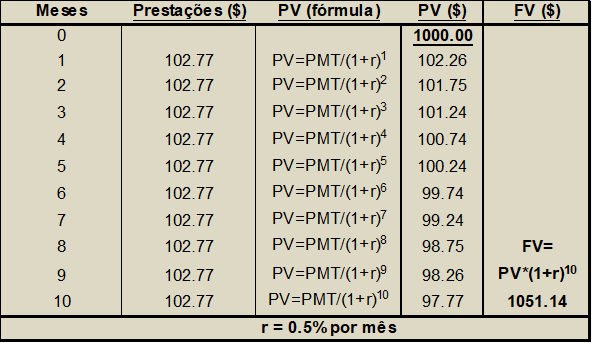
Figura 4
Genericamente temos que o valor presente de uma anuidade constante durante “n” períodos é dado por:
PV= (P / r) × ( 1 – 1 /(1 + r)n )
E, por simples manipulação algébrica, se isolarmos o valor de prestação constante “P” em função de “PV” tem-se:
P = PV × r / ( 1 – 1 /(1 + r)n )
E no exemplo acima, com PV=$1000; r= 0,5% e n=10 pode-se calcular P:
P = $1000 × 0,5% / ( 1 – 1 /(1 + 0,5%)10 ) = $102.77; e demonstrarmos na ( Figura 4) que o valor futuro equivale ao valor futuro de $51.14 acima do investimento, conforme indicamos na Figura 1.
Lembram-se da perpetuidade quando calculamos que para uma taxa de 1% ao mês, infinitas parcelas mensais de $3000 valem $300000? Pois bem em 6 anos esses mesmos 1% ao mês e as parcelas mensais de $3000 valem $153451 (ou mais da metade do valor hoje da perpetuidade). Em 40 anos com as mesmas parcelas de $3000 e uma taxa de 1% ao mês, valem hoje $297472 ou pouco mais de 99% do valor presente da perpetuidade. Ou seja, uma anuidade que ocorre a partir do primeiro mês do ano 41º vale apenas menos que 1% que o valor presente da perpetuidade. Assim taxas reais de mercado tendem a definir perpetuidade como o tempo que o ser humano está disposto a esperar pelos resultados? Será que com o aumento da expectativa de vida deveria ocorrer uma baixa na taxa de juros? Pense nisto!
Bem, caro executivo de qualquer área, apresse-se, pois em finanças o tempo é seu inimigo, a menos que você trabalhe com compras ou contas a pagar e seu fornecedor não leu este tipo de livro.
Normalmente as taxas de desconto são premissas, mas, às vezes, queremos calcular taxas “internas” de diferentes alternativas para compará-las com uma determinada “taxa de atratividade”, ou seja, nossa taxa de referência para as decisões (discutiremos esse conceito em outro capítulo). As fórmulas de cálculo das taxas de juros a partir das outras variáveis envolvem conhecimento de radiciação e logaritmos:
Cálculo das taxas de juros
Antes de tudo, quero comentar que a definição da taxa de juros embutida num fluxo de caixa, também chamada taxa interna de retorno, não deve ser usada na comparação de alternativas exclusivas, principalmente se a vida ou fluxos dessas alternativas tiverem tempos diferentes. O método correto de comparar alternativas exclusivas é definir qual delas produz um maior valor presente à taxa de atratividade ajustada ao risco do investidor.
O uso principal do cálculo da taxa interna de retorno é compará-la à taxa de investimento alternativa do investidor, ajustada ao risco, aceitando projetos onde ela é maior. É importante notar que esta taxa interna de retorno é única apenas se ocorrer no início uma saída de caixa e a partir daí ocorrerem fluxos positivos. Se houver caixa negativo em anos futuros a anos positivos, o fluxo apresentará mais de uma resposta como sua taxa interna de retorno. O que segue é esta matemática.
Primeiramente vamos calcular taxa de juros ou de atratividade dados o Valor Presente na data t0 e o Valor Futuro na data tn.
Já vimos que: FVtn = PVt0 × (1 + r )n e portanto (1 + r )n = ( FVtn / PVt0 )
Portanto se (1 + r )n = ( FVtn / PVt0 ) => r = ( FVtn / PVt0 )1/n
r = ( FVtn / PVt0 )1/n – 1
Na perpetuidade é ainda mais fácil calcular a taxa de juros a partir do valor presente PVt0 e da parcela perpétua P:
Sabemos que:
PVt0 = P / r
Portanto r = P / PVt0
Em seguida a relação entre taxa de juros e n parcelas iguais e discretas consecutivas:
Mostramos que:P = PV × r / ( 1 – 1 /(1 + r)n )
Esta equação obviamente tem uma única solução para r dados P, PV e n, entretanto não há uma solução algébrica simples devido ao exponencial n.
Vários métodos são apresentados para aproximar o valor de r em calculadoras financeiras. O Excel tem formulas iterativas que aproximam esta solução. Abaixo indico um exemplo de como isto pode ser feito mesmo sem as fórmulas iterativas já programadas:
Suponha que ao investir $1000 você receba 10 parcelas de $110. Qual a taxa de juros envolvida:
Escrevam no Excel as fórmulas assim, onde delta é a diferença entre a segunda e quinta colunas:
r=5% foi um chute e se mostrou muito alto, portanto iremos reduzir este chute até que o delta se aproxime de zero e teremos a resposta.
Bem perto, não é?
Também podemos desenhar o gráfico ( Figura 5) desenhar r x Delta e ver quando ele cruza o eixo Delta = zero, um pouco acima de 0,897%.
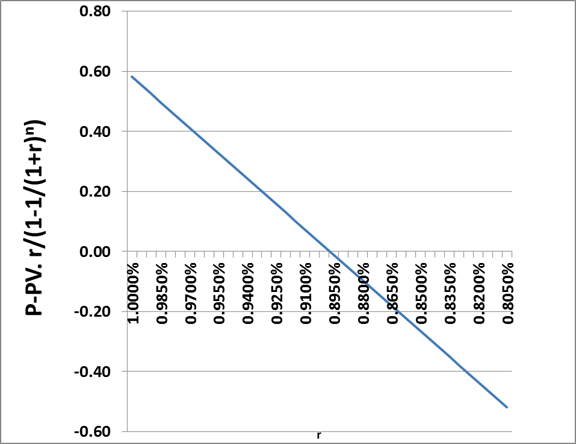
| Figura 5 |
Sumário das fórmulas de matemática financeira com fluxos discretos
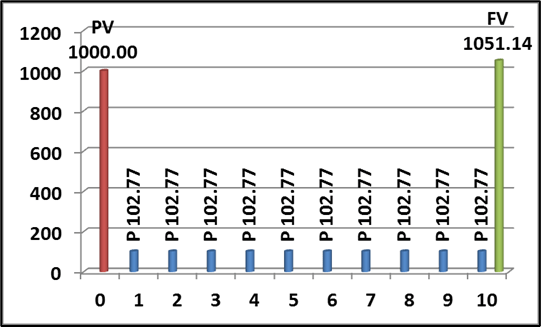
Figura 6
Sendo:
PV = valor presente no início dos períodos
FV = valor futuro no final dos períodos
n = número de períodos
r = taxa de juros reais ou taxa de atratividade por período
P = parcelas uniformes ocorrendo durante todos os períodos
Os fluxos azuis, vermelhos e verdes se equivalem a uma taxa de juros de 5% ao período.
Valor Futuro a partir de um Valor Presente: FV = PV × (1 + r )n
Valor Presente a partir de um Valor Futuro: PV = FV / (1 + r )n
Valor da Prestação Uniforme a partir do Valor Presente: P = PV × r / ( 1 – 1 / (1+r)n )
Valor da Prestação Uniforme a partir do VF: P = (FV / (1 + r )n ) × r / ( 1 – 1 / (1+r)n )
Valor Presente a partir de Prestação Uniforme: PV= (P / r) × ( 1 – 1 / (1 + r)n )
Valor Futuro a partir de Prestação Uniforme: FV = (P / r) × ( 1 – 1 / (1 + r)n ) x (1 + r )n
Valor Presente de uma perpetuidade P (n = ∞): PV = P / r
Taxa de Retornoa partir de n, PVt0 e FVtn: r = ( FVtn / PVt0 )1/n – 1
Taxa de Retorno a partir de PVt0 e uma perpetuidade discreta P: r = P / PVt0
Deixe um comentário